Предмет: Математика,
автор: klichevaviktoriya
Найти производные )))
Прошу помощи От умных людей
Приложения:
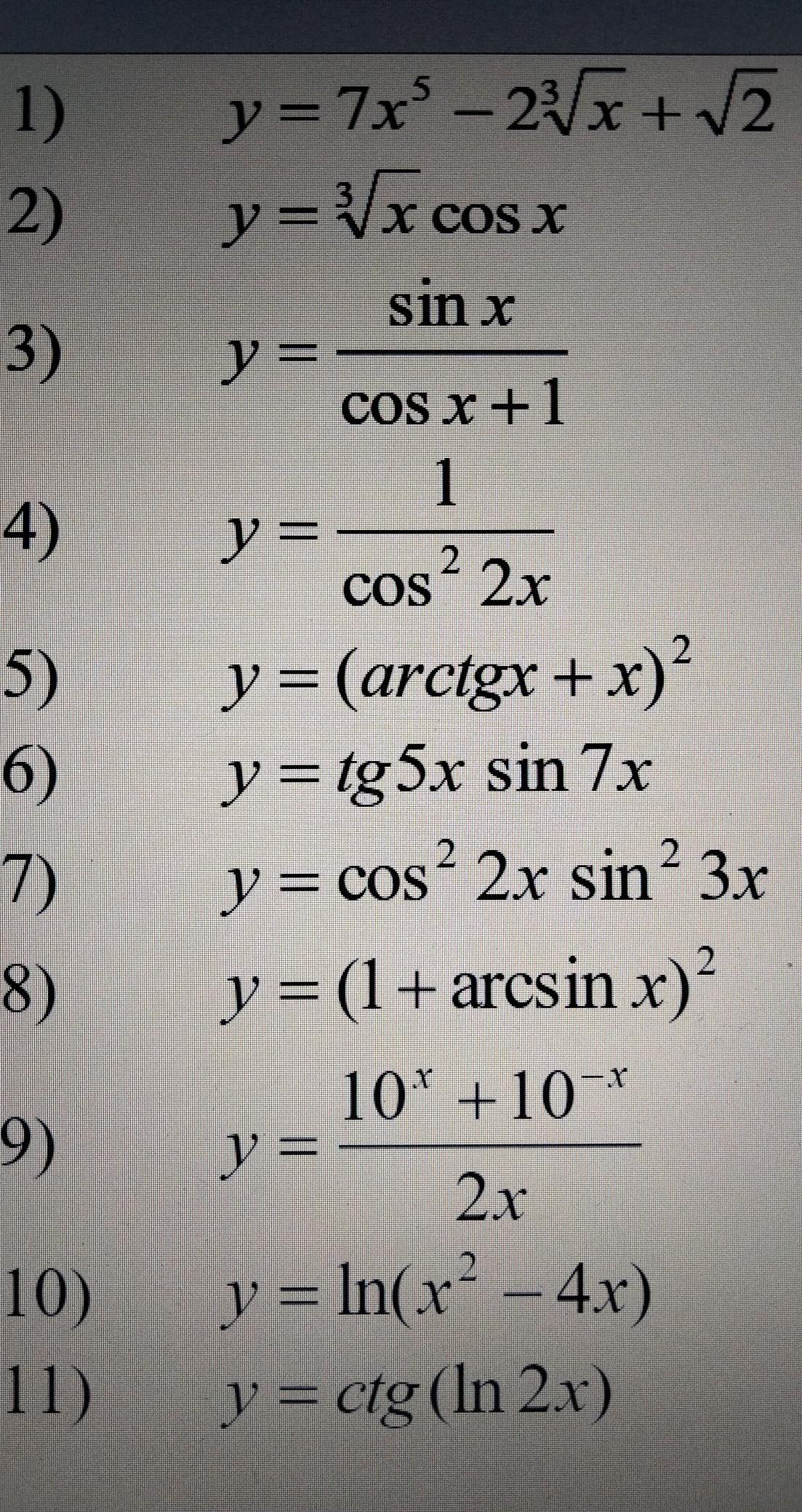
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: noginaalina219
Предмет: Алгебра,
автор: viviq12338
Предмет: Геометрия,
автор: rebelkanalRebezel
Предмет: Математика,
автор: Weronika2017
Предмет: Математика,
автор: maksi8