Предмет: Алгебра,
автор: grattttt
Решите логарифмическое неравенство!!!!!!!!!!
Приложения:
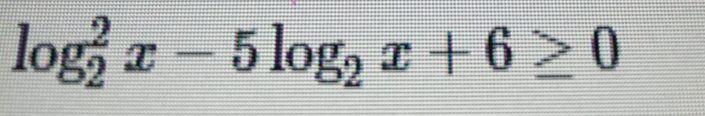
manskill586:
щя
Ответы
Автор ответа:
1
Ответ:
замена:
t принадлежит (- беск; 2]U[3;+ беск).
Одз: x>0.
Все пересекаем, получаем:
х принадлежит (0;4]U[8;+ беск).
Похожие вопросы
Предмет: Русский язык,
автор: isaeva1428
Предмет: Математика,
автор: varvaragor50
Предмет: Русский язык,
автор: oksana88v
Предмет: Биология,
автор: Аноним
Предмет: Биология,
автор: Фарида060