Предмет: Алгебра,
автор: grattttt
Решите логарифмическое неравенство срочно!!!!!!!!
Приложения:
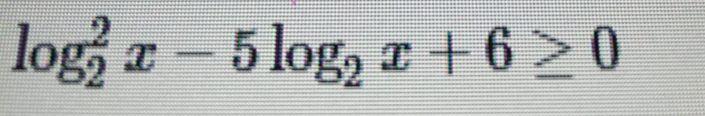
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: История,
автор: миша11110
Предмет: Русский язык,
автор: Vladislav22812
Предмет: Математика,
автор: Sofiko32
Предмет: Математика,
автор: Крутая195023
Предмет: Математика,
автор: glushkova80