Предмет: Математика,
автор: saakyangaren
Помогите пожалуйста решить.
1)Найдите общее решение уравнения:
y'= y cos x
2)Найдите частное решение уравнения при заданных условиях:
y'+at^3=0 если t=0, то y=5, a= const
3) Найдите производную функции:
y=x*sin2x
4) Найдите производную сложной функции:
y=e^x/ x^5
Приложения:
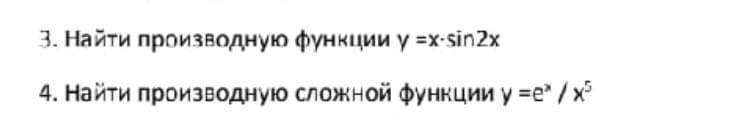

Ответы
Автор ответа:
0
Ответ:
Приложения:


Похожие вопросы
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: ptv2020
Предмет: История,
автор: ilyasgaliev01
Предмет: Алгебра,
автор: prestigpad