Предмет: Математика,
автор: nastkan95
Проинтегрировать функции заменой переменной:
Приложения:
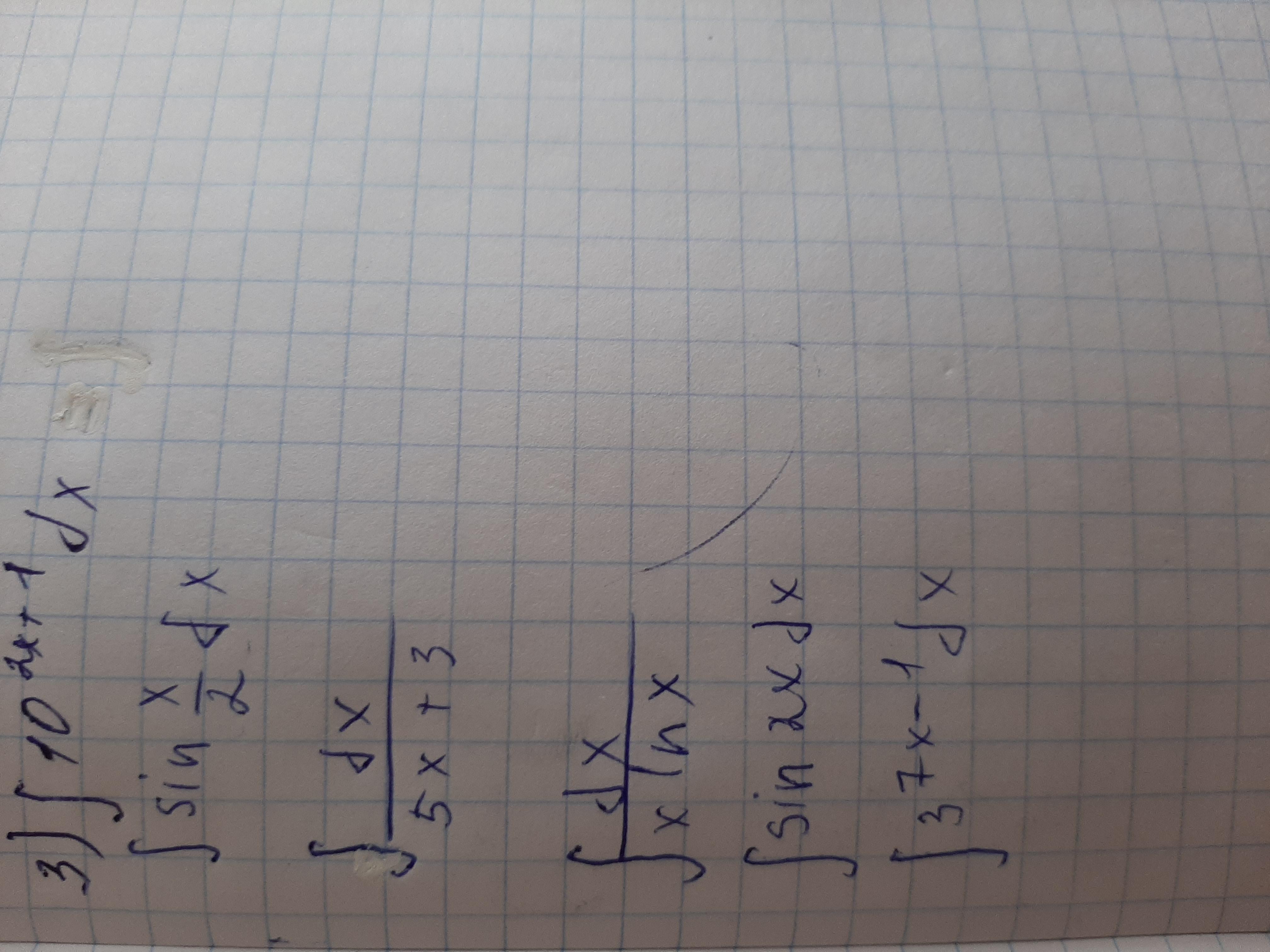
pushpull:
я бы решила, но запись не понятна, что в первом в степени, что в третьем знаменатель..... напишите в понятном виде. лучше на листике и прикрепите файл
решила
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
1)
2)
3)
4)
5)
6)
Похожие вопросы
Предмет: Математика,
автор: surovitski
Предмет: Английский язык,
автор: Софья85
Предмет: Математика,
автор: bobretsowaanna
Предмет: Биология,
автор: 20031101
Предмет: Обществознание,
автор: ganskijartem