Question

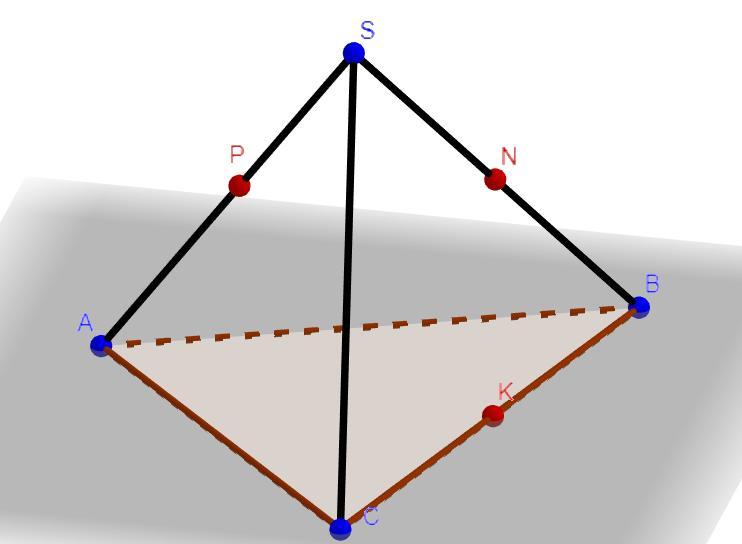
У правильному тетраєдрі SАВС, всі ребра якого дорівнюють 2корінь3,
знайдіть площу перерізу, що проходить через ребро SB і середину
ребра АС.

Answer 1

В правильном тетраэдре все грани равны.

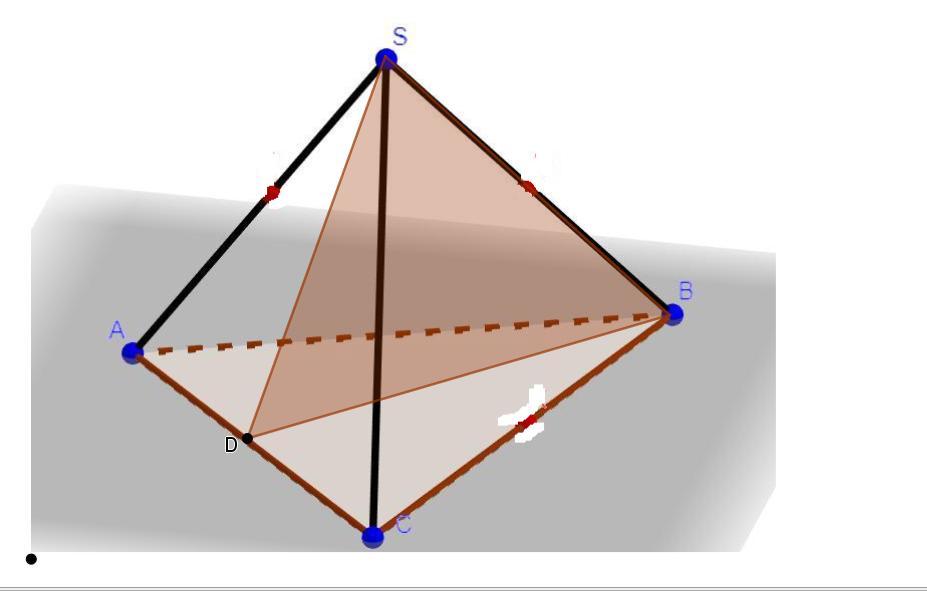
Заданное сечение проходим через боковое ребро SB,  высоту ho = BD основания и апофему A = SD боковой грани.

A = ho = a*cos30° = 2√3*(√3/2) = 3.

S = (1/2)h(D_SB)*a = (1/2)*√(A² - (a/2)²)*a = (1/2)*√(9 - (2√3)/2)²)*(2√3) =

  = (1/2)*√(9 - 3)*(2√3) = 3√2.