Предмет: Математика,
автор: anabelfett
Помогите решить.. Очень срочно..
Приложения:
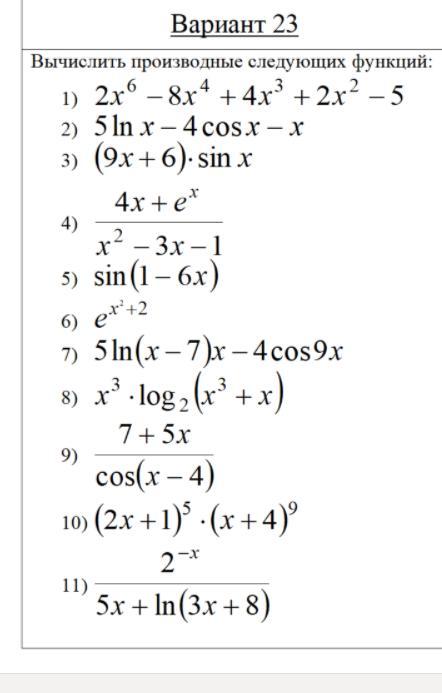
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Химия,
автор: anya5378
Предмет: Алгебра,
автор: Vlad0s98
Предмет: Геометрия,
автор: kaiserlv55
Предмет: Математика,
автор: 0671152543
Предмет: Математика,
автор: маруся493кс