Предмет: Алгебра,
автор: flaimoh
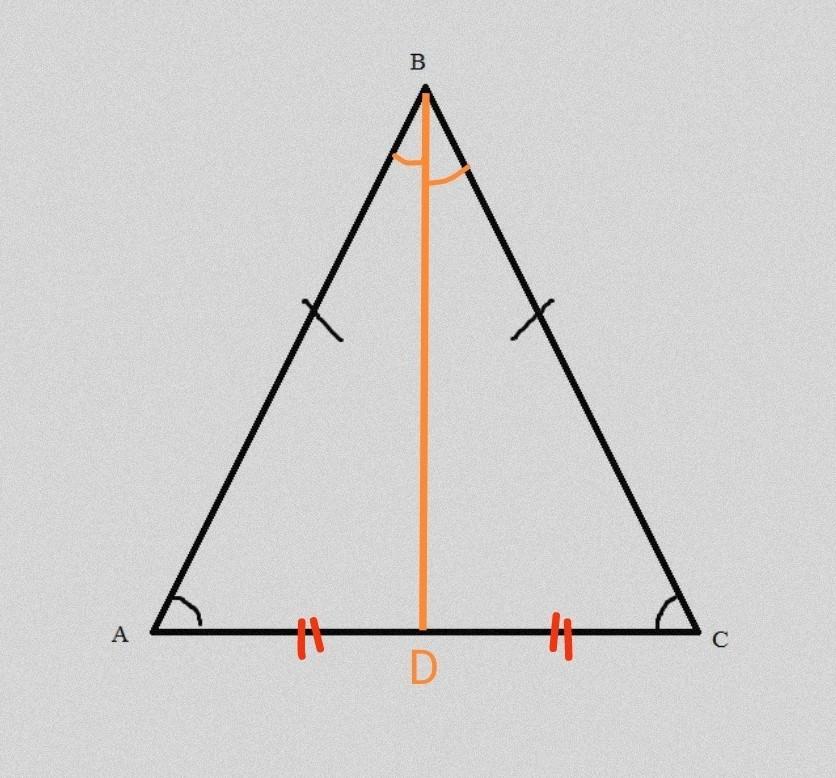
В равнобедренном треугольнике с длиной основания 12 cм проведена биссектриса угла ∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой, и определи длину отрезка AD. ПРОШУ СРОЧНО
Ответы
Автор ответа:
2
АС = 6 см
Объяснение:
∆ABD = ∆BDC по 2 признаку (АВ=ВС и ∠ВАD = ∠BCD т.к. ∆ABC - равнобедренный; ∠ABD = ∠CBD т. к. BD - биссектриса ∆ABC) => AD=DC (как равные элементы) => BD - медиана
Раз AD = DC и АС = AD+DC => АС = 2AD => AD = АС/2 => AD = 12/2 = 6см
Приложения:
Похожие вопросы
Предмет: Биология,
автор: buraevat
Предмет: Русский язык,
автор: sultansadraliev1
Предмет: Русский язык,
автор: 2601831
Предмет: Алгебра,
автор: alex27hab
Предмет: Математика,
автор: Maximus193883