Предмет: Геометрия,
автор: maikoz
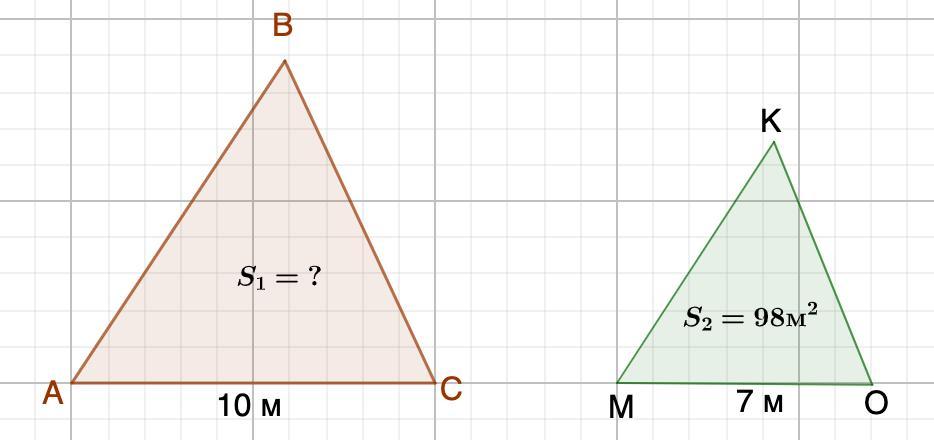
Даны два подобных многоугольника. Площадь меньшего многоугольника равна 98 м2. Соответствующие стороны многоугольника равны 7 м и 10 м. Найди площадь второго многоугольника.
427qwefghjnm:
200
Ответы
Автор ответа:
1
Ответ:
200 м²
Объяснение:
Дано: ΔАВС~ΔМКО
S₂=98 м²
АС=10 м; МО=7 м.
Найти: S₁-?
Решение:
Коэффициент подобия — число k, равное отношению сходственных сторон подобных треугольников.
Площади подобных треугольников относятся как квадрат коэффициента подобия - k²
Найдем k:
Найдем S₁:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: maruanna
Предмет: Литература,
автор: Неон1
Предмет: География,
автор: jazz124
Предмет: Литература,
автор: SALATt587
Предмет: Математика,
автор: xgji126