Предмет: Математика,
автор: aldragn29
Решите показательные уравнения
Приложения:
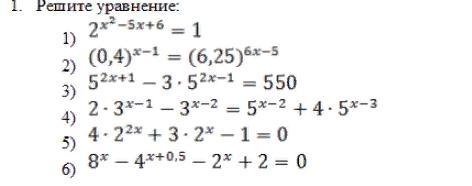
Ответы
Автор ответа:
1
Ответ:
Ответ: 2,3.
Замена:
нет корней.
Ответ:-2.
Замена:
корень -1 не подходит.
Ответ: 0;1.
Похожие вопросы
Предмет: Другие предметы,
автор: 0ксения0
Предмет: Математика,
автор: shkhavumova
Предмет: Математика,
автор: слонячий
Предмет: Математика,
автор: муня16
Предмет: История,
автор: teluhina804216