Предмет: Математика,
автор: kristinant04
По значению одной тригонометрической функции найти значение остальных трех
Приложения:
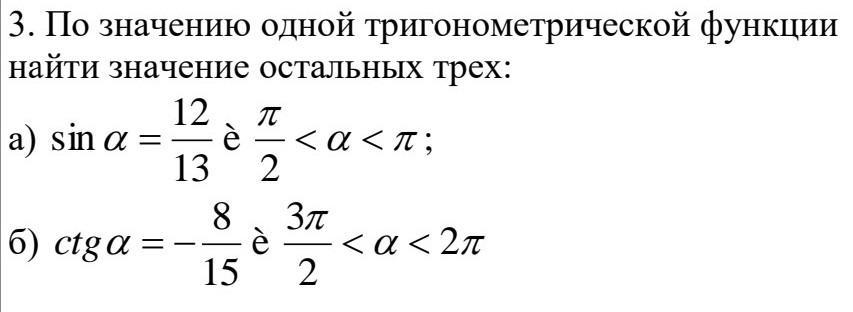
Ответы
Автор ответа:
2
Ответ:
1.
а принадлежит II четверти => косинус, тангенс и котангенс отрицательные.
2.
IV четверть => тангенс, синус отриц, косинус положительный.
Используем формулу:
(знак перед корнем выбираем в зависимости от угла)
Похожие вопросы
Предмет: География,
автор: tanya7921
Предмет: Русский язык,
автор: oxzix666
Предмет: Математика,
автор: dimasviridov2
Предмет: Математика,
автор: 1234814
Предмет: Математика,
автор: KNAZ90