Предмет: Математика,
автор: Geographist
Интеграл и Предел по правилу Лопиталя. Помогите люди добрые. Только те кто понимает
Приложения:
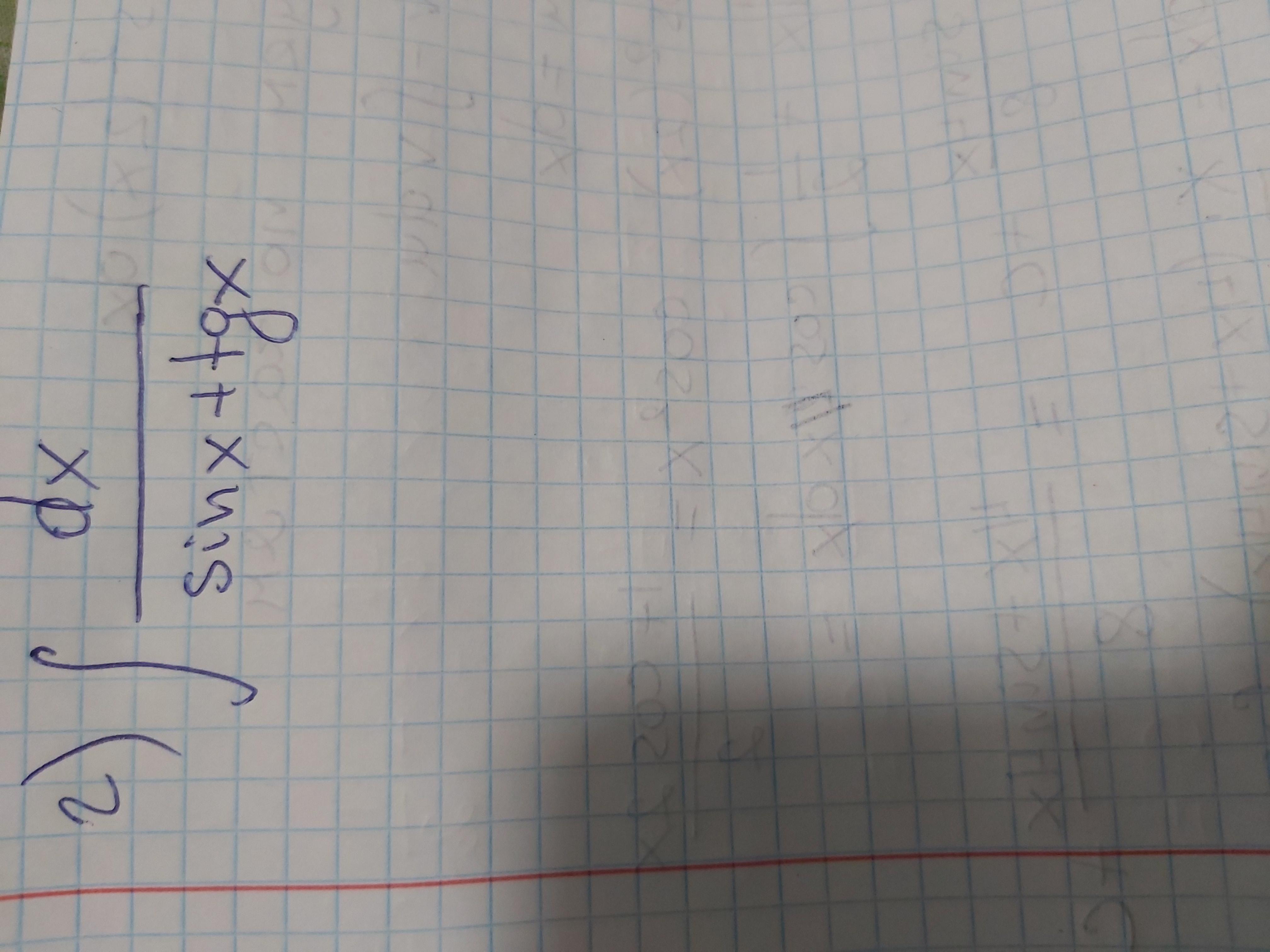
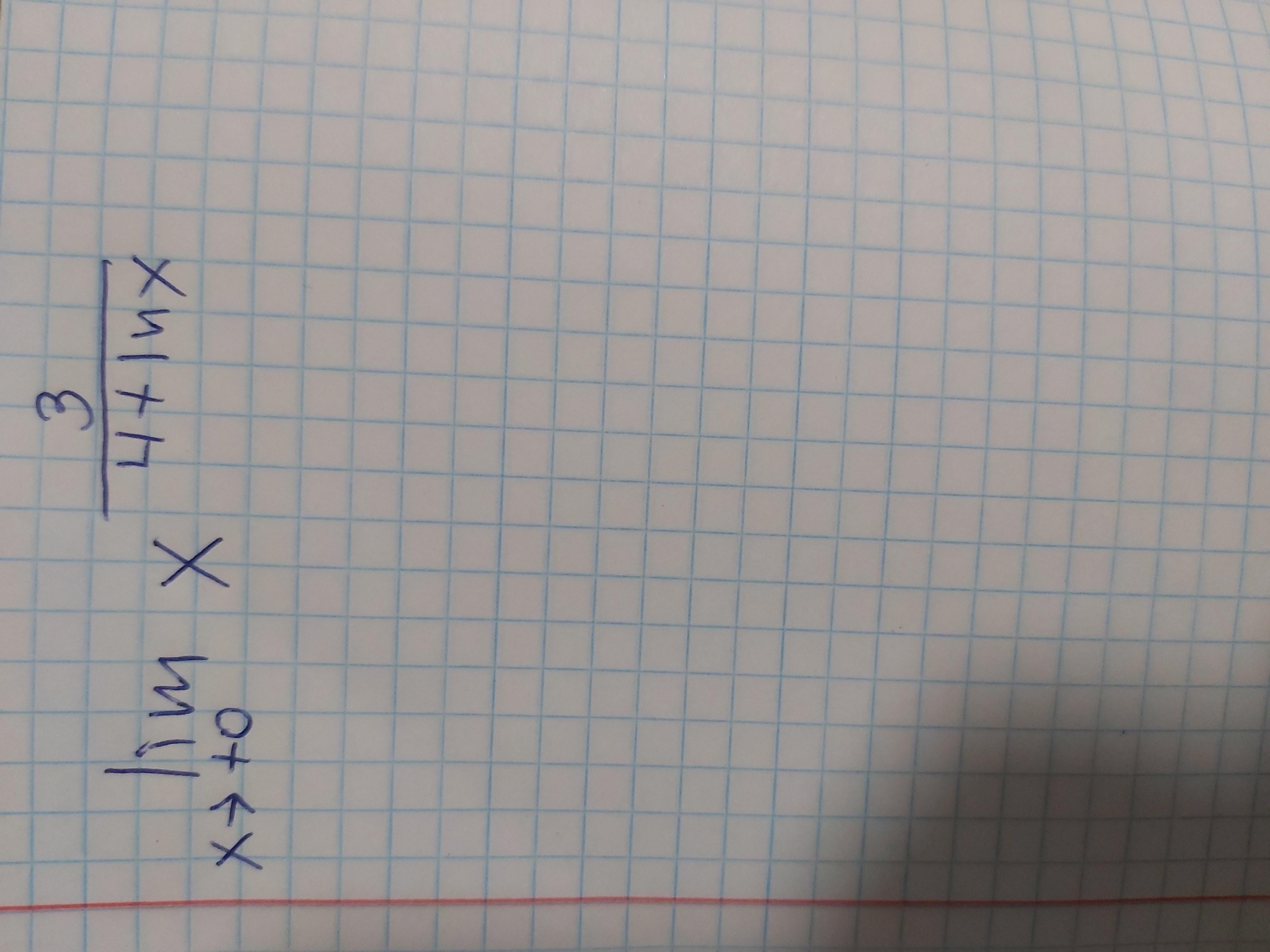
Ответы
Автор ответа:
1
Приложения:
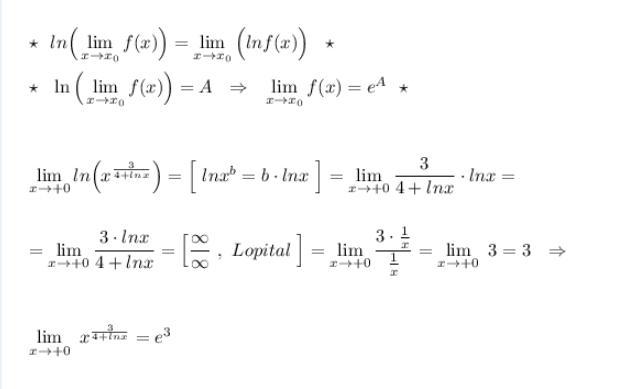
lasl42:
помогите кто то с математикой:')
Похожие вопросы
Предмет: Биология,
автор: alna29012003
Предмет: Физика,
автор: irinachernysho1
Предмет: Геометрия,
автор: аня7399
Предмет: Литература,
автор: svetl1091974