Предмет: Алгебра,
автор: iheto3696
Срочно! Сравните два лёгких логарифма!
Приложения:
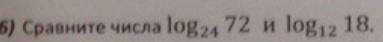
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: alianaarabkhan
Предмет: Математика,
автор: ulanasergo9
Предмет: Английский язык,
автор: ytevka163
Предмет: Химия,
автор: natashapetriko
Предмет: Литература,
автор: alexei000007