Предмет: Математика,
автор: nins12
вычислить производную сложной функции, используя правила дифференцирования сложной функции.
задание на картинке
Приложения:
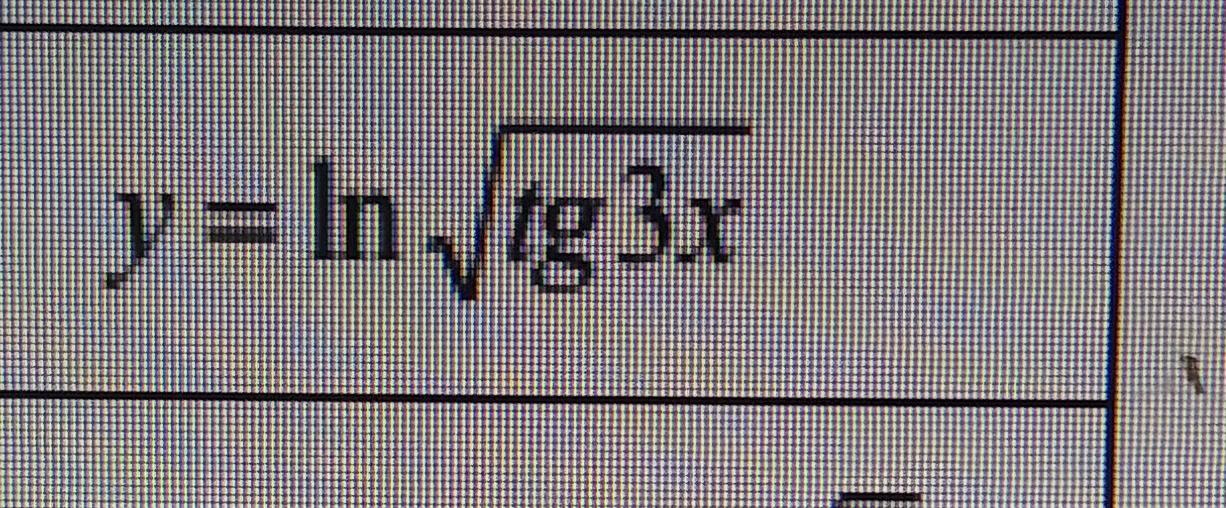
Ответы
Автор ответа:
0
Ответ:
tan(x) - это tg(x)
Похожие вопросы
Предмет: Химия,
автор: AigulkaKomarova
Предмет: Английский язык,
автор: marchukviktoria
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: timosevskijdimozdfyr
Предмет: Математика,
автор: АлисМяу