Question

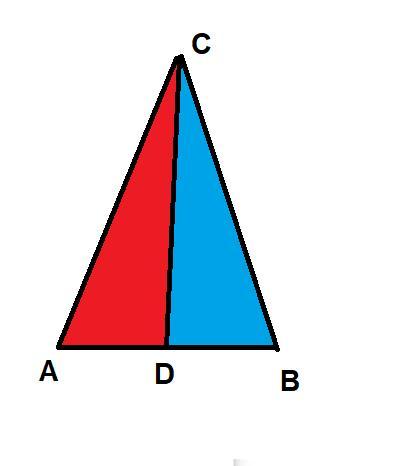
В треугольнике ABC проведены медианы AM и CD. Периметры треугольников ACD и BCD равны, а периметр треугольника ABC равен 32 см. Найдите стороны треугольника ABC, если АС : АВ =5:6(помогите пж)

Answer 1

Ответ:

AC = BC = 10см, AB = 12см

Объяснение:

Посмотрим, в каком случае медиана делит треугольник на 2 треугольника с равным периметром (в данном случае - медиана CD).

P(ACD) = P(BCD)

AC + CD + DA = BC + CD + DB

AC + DA = BC + DB

AC = BC (т.к. DA = DB по определению медианы).

Пусть, AC = BC = 5x

AC:AB = 5:6 ⇒ AB = 6x

AC + BC + AB = 32см (по условию)

5x + 5x + 6x = 32см

16x = 32см

x = 2см

AC = BC = 10см, AB = 12см