Предмет: Математика,
автор: www1782
Помогите пожалуйста решить интеграл.Очень срочно,спасибо!
Приложения:
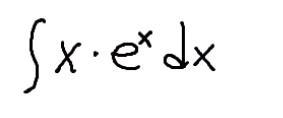
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Интегрируем по частям, общая формула:
Принимаем:
Тогда , т.к.
Получаем:
Проверка:
Получилась подынтегральная функция, значит, все сделано верно.
Похожие вопросы
Предмет: Английский язык,
автор: albertdarchiev
Предмет: Алгебра,
автор: cergoM
Предмет: Информатика,
автор: gfyhejnjk23
Предмет: Литература,
автор: Dimaxes
Предмет: Математика,
автор: Настька210107