Помогите, даю 15 баллов за 2 задания
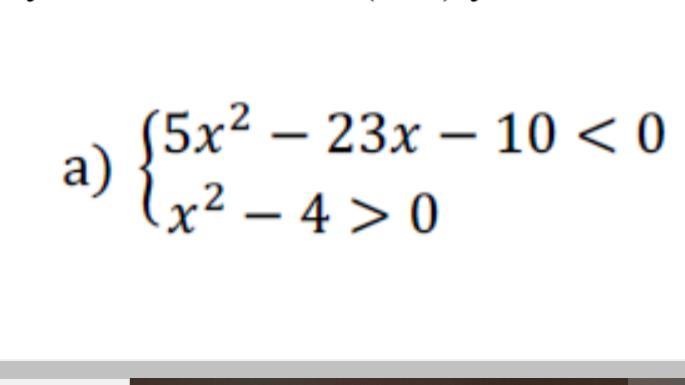
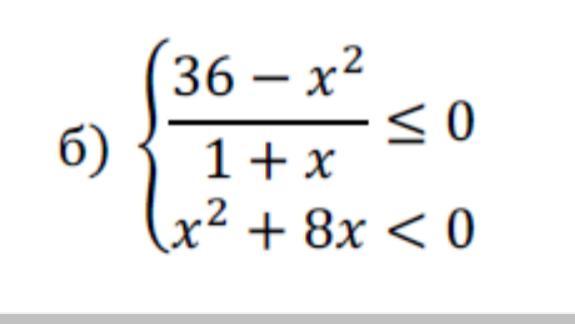
Ответы
Ответ:
Объяснение:
1-я система неравенств:
5x²-23x-10<0
x²-4>0
1-е неравенство.
5x²-23x-10<0
Допустим:
5x²-23x-10=0; D=529+200=729
x₁=(23-27)/10=-4/10=-0,4
x₂=(23+27)/10=50/10=5
Наносим для этого неравенства точки на ось x и выберем точку из любого интервала, например, 0:
5·0²-23·0-10<0; -10<0
Следовательно, знак на интервале, в котором лежит точка 0 будет -.
+ - +
-----.-----------------.-----------> x
-0,4 5
-0,4<x<5⇒x∈(-0,4; 5) для 1-го неравенства.
2-е неравенство.
x²-4>0; (x-2)(x+2)>0
Допустим:
(x-2)(x+2)=0
x-2=0; x₁=2
x+2=0; x₂=-2
Наносим для этого неравенства точки на ось x и выберем точку из любого интервала, например, 0:
0²-4>0; -4<0
Следовательно, знак на интервале, в котором лежит точка 0 будет -.
+ - +
---------.--------------.------------> x
-2 2
(-∞<x₂<-2)∨(2<x₁<+∞)⇒x∈(-∞; -2)∪(2; +∞) для 2-го неравенства.
А теперь выводим окончательный ответ: x∈(2; 5).
2-я система неравенств:
(36-x²)/(1+x)≤0
x²+8x<0
1-е неравенство.
Переходим к методу интервалов:
(6-x)(6+x)≤0
1+x≠0
Переходим к уравнению:
(6-x)(6+x)(1+x)=0
6-x=0; x₁=6
6+x=0; x₂=-6
1+x=0; x₃=-1
Учитываем дополнительное требование:
1+x≠0; x≠-1
Наносим для этого неравенства точки на ось x и выберем точку из любого интервала, например, 0:
(36-0²)/(1+0)≤0; 36>0
Следовательно, знак на интервале, в котором лежит точка 0 будет +.
+ - + -
----------.-----------.-----------------.--------------> x
-6 -1 6
[-6<x<-1)∨(6<x<+∞)⇒x∈[-6; -1)∪[6; +∞) для 1-го неравенства.
2-е неравенство.
x²+8x<0; x(x+8)<0
Допустим:
x(x+8)=0
x₁=0
x+8=0; x₂=-8
Наносим для этого неравенства точки на ось x и выберем точку из любого интервала, например, 1:
1²+8·1<0; 9>0
Следовательно, знак на интервале, в котором лежит точка 1 будет +.
+ - +
------------.----------------------.------------------> x
-8 0
-8<x<0⇒x∈(-8; 0) для 2-го неравенства.
Окончательный ответ: x∈[-6; -1).