Предмет: Геометрия,
автор: alanabai2001j
Пропорциональные отрезки в прямоугольном треугольнике
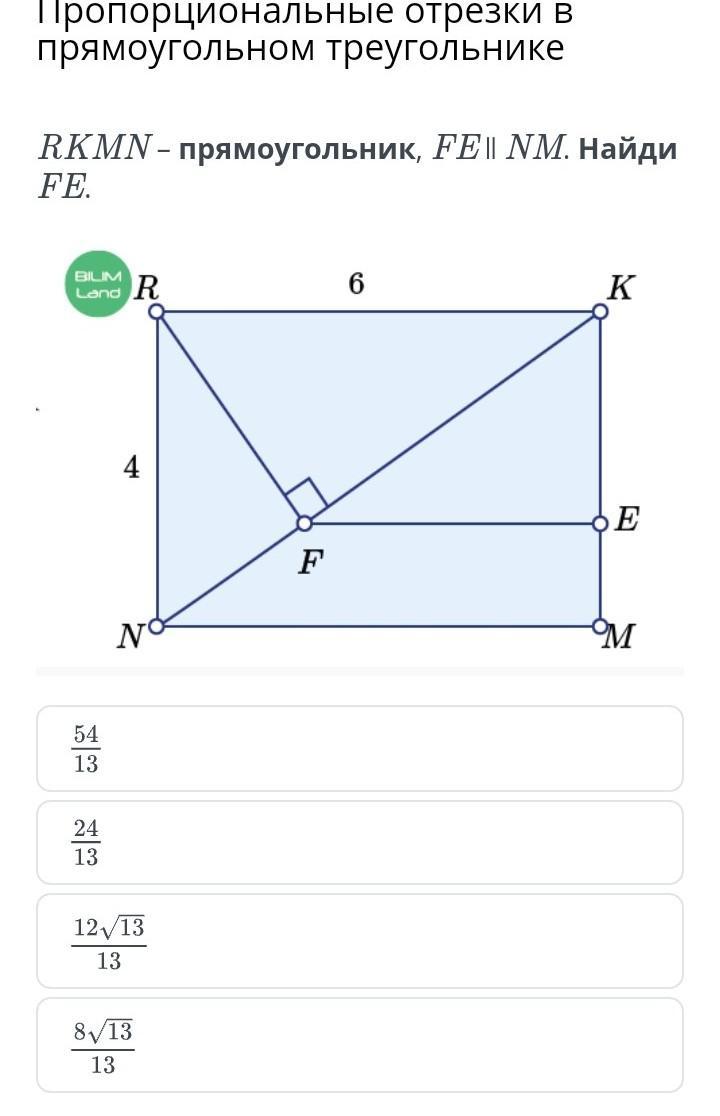
RKMN – прямоугольник, FE ∥ NM. Найди FE.
Приложения:
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Дано: NRKM - прямоугольник;
FE || NM; NR=4; RK=6
Найти: FE
Решение:
Квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу.
⇒ NR²=NF·NK; RK²=KF·NK
Выразим NF и FK:
Найдем отношение этих отрезков:
Рассмотрим ΔNKM и ΔFKE
FE || NM (условие)
Если две стороны треугольника пересекает прямая, параллельная третьей стороне, то она отсекает треугольник, подобный данному.
⇒ ΔNKM ~ ΔFKE
Пусть FK=9x ⇒ NF=9x+4x=13x
Составим пропорцию:
Похожие вопросы
Предмет: Биология,
автор: nonstos
Предмет: Русский язык,
автор: manucharyane
Предмет: Другие предметы,
автор: taxir007007
Предмет: Математика,
автор: esareff
Предмет: Геометрия,
автор: Кларос