Предмет: Геометрия,
автор: seva1012
Ребят СРОЧНО помогите с геометрией
9 класс
Синус косинус и тангенс
Приложения:
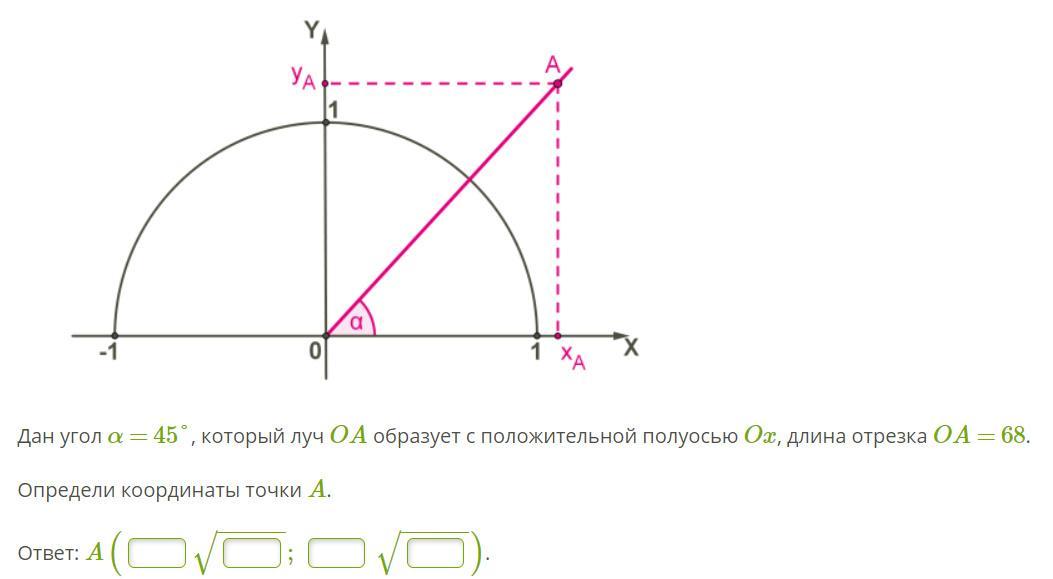
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Имеем две точки:
Найдём координаты вектора OA:
Теперь найдём длину вектора OA:
По условию, длина вектора OA составляет 68:
Из последнего равенства можно сделать вывод, что треугольник
прямоугольный.
Найдём катет, противолежащий углу α:
Найдём катет, прилежащий углу α:
Из рисунка видно, что
Так как оба катета выходят из точки O (0; 0), то
Похожие вопросы
Предмет: Литература,
автор: настюша1121
Предмет: Биология,
автор: TUSJ5
Предмет: Математика,
автор: dumkina44
Предмет: Обществознание,
автор: Apostol26
Предмет: Математика,
автор: 111111вау