Question

Помогите, пожалуйста, с геометрией

Answer 1

Ответ:

3,5 см

Объяснение:

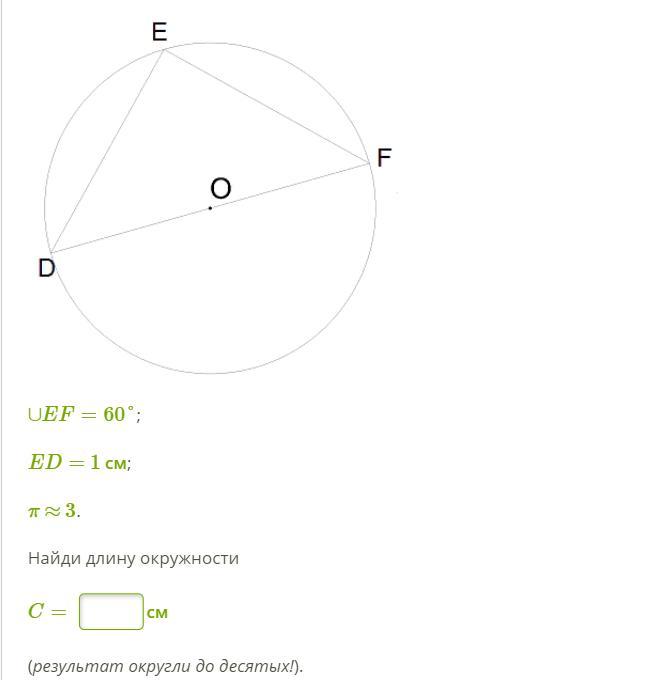
1) ∠ E = 90°, т.к. опирается на диаметр DF.

2) ∠ D = 1/2 дуги EF, на которую опирается:

60 : 2 = 30°.

3) В прямоугольном треугольнике DEF катет ED равен гипотенузе DF, умноженной на косинус угла, прилежащего к этому катету:

ED = DF * соs 30°,

1 = DF * √3/2,

откуда  

DF = 2/√3.

4) Длина окружности равна произведению её диаметра на число "пи", которое, согласно условию задачи, равно 3:

C = 3 * 2/√3  = 6 /√3 = 6 : 1,732 ≈ 3,5 см

Ответ: 3,5 см

Answer 2

Ответ:

3,5

.....

РЕШЕНИЕ:

C=πd

d- диаметр окружности

......

градусная мера угла на которого опирается дуга равна её половине тоесть

∠EDF=½∪EF=30°

на рисунку видно что DF - диаметр

значить ∪FD=180°

и

∪ ED=180°-60°=120°

∠EFD=½∪ ED=60°

сумма углов треугольника 180°

значит ∠DEF=180°-(60°+30°)=90°

нам нужно найти DF ну или гипотенузу треугольника ЕDF ну или диаметр окружности

у нас известно ED и все углы

$\cos∠EDF = \cos30° = \frac{ED}{DF}$

$\frac{ \sqrt{3} }{2} = \frac{1}{DF}$

$DF = \frac{2}{ \sqrt{3} }$

$С= \frac{2}{ \sqrt{3} } \times 3 = 2 \sqrt{3}$

2√3 это приблизительно 3,5