Question

Помогите, пожалуйста. Основанием прямой четырехугольной призмы является
равнобедренная трапеция с основаниями 6 см и 12 см и боковой
стороной 5 см. Высота призмы относится к высоте трапеции как 2:1.
Найти: площадь основания, площадь боковой поверхности, площадь
полной поверхности, объем призмы.

Answer 1

Ответ:

Sосн=36см²

Sбок=224см²

Sпол=296см²

V=288cм³

Объяснение:

Дано

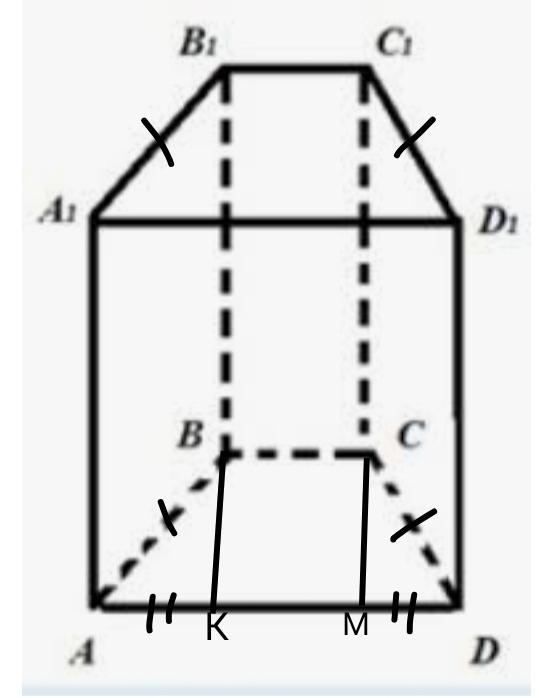
ABCDA1B1C1D1- призма

ABCD- трапеция

АВ=CD=5см боковая сторона трапеции.

ВС=6см верхнее основание трапеции.

АD=12см нижнее основание трапеции.

В1В:ВК=2:1.

Sосн.=?

Sбок=?

Sпол=?

V=?

Решение.

АК=МD

AK=(AD-BC)/2=(12-6)/2=6/2=3 см.

∆АВК- прямоугольный (<ВКА=90°)

По теореме Пифагора найдем высоту трапеции.

ВК²=АВ²-АК²=5²-3²=25-9=16см.

ВК=√16=4 см высота трапеции.

Sосн=ВК(ВС+AD)/2=4*(6+12)/2=4*18/2=

=36см² площадь трапеции.

ВВ1=2*ВК=2*4=8см высота призмы.

Росн=АВ*2+ВС+AD=5*2+6+12=10+18=28см периметр трапеции.

Sбок=Росн*ВВ1=28*8=224см² площадь боковой поверхности призмы.

Sпол=2Sосн+Sбок=2*36+224=72+224=

=296 см² площадь полной поверхности призмы.

V=Sосн*ВВ1=36*8=288см³ объем призмы.