Question

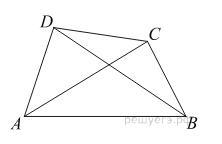
Найдите периметр четырехугольника, вершинами которого являются середины сторон выпуклого четырехугольника ABCD, если диагонали ABCD равны 4 и 6.

Answer 1

Ответ:

10

Пошаговое объяснение:

Стороны искомого четырехугольника равны средним линиям треугольников, образуемых диагоналями и сторонами данного четырехугольника. Таким образом, стороны искомого четырехугольника равны половинам диагоналей. Соответственно,

$P=\frac{1}{2\\\\} AC + \frac{1}{2\\\\} CA + \frac{1}{2\\\\} DB + \frac{1}{2\\\\} BD = 2 + 2 + 3 + 3 = 10$