Question

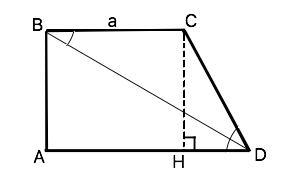
В прямоугольной трапеции ABCD (BC ║ AD) ∠A – прямой, BC = a, угол BCD в 2 раза больше угла CDA, диагональ BD – биссектриса ∠CDA. Найдите основание AD.
С решением

Answer 1

Ответ: AD=1,5 a

Объяснение:  Примем угол АDС=х. Тогда по условию угол ВСD=2х.

 Сумма внутренних односторонних углов при пересечении параллельных  прямых ( ВС и AD) секущей (CD) равна 180°.

∠ВСD +∠CDA=2х+х=180°=>

х=180°:3=60°

СВD=∠BDA (накрестлежащие).

      Биссектриса ВD делит угол CDA пополам. ∠СВD=∠BDС

∆ ВСD - равнобедренный по равенству углов при основании .

CD=BC=a;

СН -высота трапеции. ∆СDH - прямоугольный.  

∠DCH=180°-90°-60°=30°.

Катет HD противолежит углу 30° и равен половине гипотенузы CD. HD=0,5a.

АН=ВС=а

AD=a+0,5a=1,5 a.