Предмет: Алгебра,
автор: csgoglobaloff2020
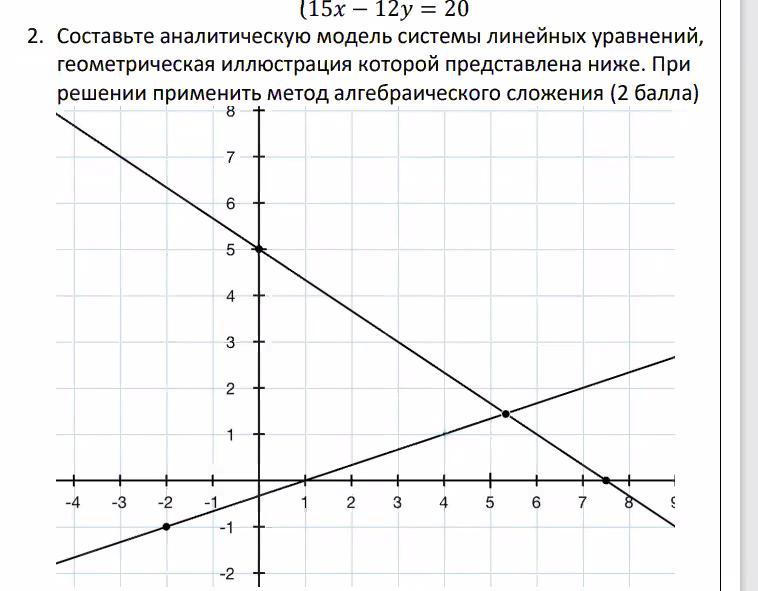
40 баллов прикрепленный файл,1 задача 7 класс
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
На графике представлены функции вида:
Вычислим уравнения прямых:
Тогда аналитическая модель системы линейных уравнений выглядит следующим образом:
Вычитаем второе из первого и получаем:
Подставляем найденный x в любое из уравнений и находим y:
Похожие вопросы
Предмет: Математика,
автор: ni1703
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: kirakosyan71
Предмет: Литература,
автор: azamat0071
Предмет: Математика,
автор: dashaminori