Предмет: Алгебра,
автор: mowswlaj
Используя таблицу производных и основные правила дифференцирования, найти производные функций
Приложения:
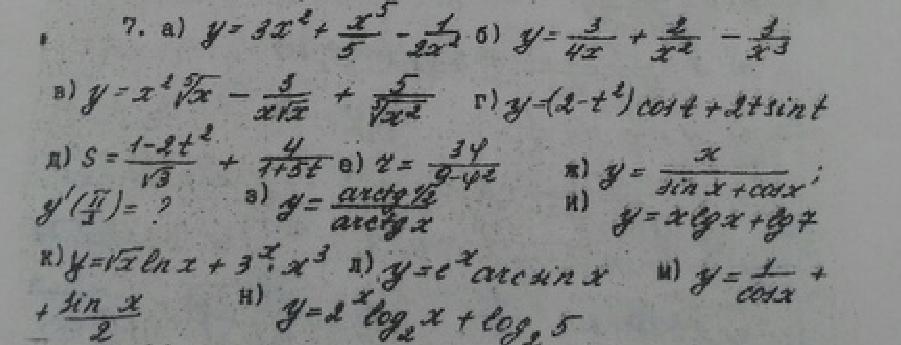
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: История,
автор: SonyaMyacina
Предмет: Биология,
автор: mery1305
Предмет: Математика,
автор: про100Юля1
Предмет: Математика,
автор: рлмыьоылр
Предмет: Математика,
автор: sadlily10Liliya