Question

Снаряд, выпущенный вертикально вверх, разорвался в верхней точке траектории. Первый осколок массой 4 кг приобрел скорость 200 м/с, направленную горизонтально. Второй осколок массой 9 кг полетел вверх со скоростью 50 м/с. Какова скорость третьего осколка, если его масса равна 8 кг?ответ округлить до целых​

Answer 1

Ответ:

$v_{3} = 115$ м/c

Объяснение:

Дано:

$m_{1} = 4$ кг

$v_{1} = 200$ м/с

$m_{2} = 9$ кг

$v_{2} = 50$ м/с

$m_{3} = 8$ кг

Найти:

$v_{3} - ?$

-----------------------------

Решение:

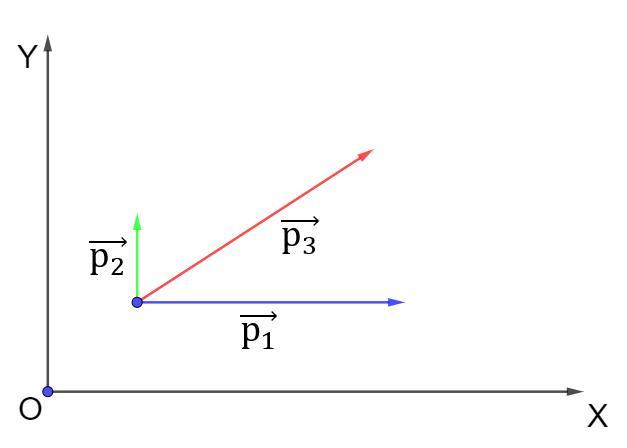
Третий осколок полетит в направлении обратному сумме импульсов первых двух осколков.

По закону сохранения импульса:

$\overrightarrow{p_{1}} + \overrightarrow{p_{2}} + \overrightarrow{p_{3}} = 0$

$m_{1}\overrightarrow{v_{1}} + m_{2}\overrightarrow{v_{2}} + m_{3}\overrightarrow{v_{3}} = 0$

$OX: m_{1}v_{1} + m_{3}v_{3_{\displaystyle x}} = 0;m_{3}v_{3_{\displaystyle x}} = -m_{1}v_{1}$

$OY: m_{2}v_{2} + m_{3}v_{3_{\displaystyle y}} = 0;m_{3}v_{3_{\displaystyle y}} =- m_{2}v_{2}$

$\displaystyle \left \{ {{m_{3}v_{3_{\displaystyle x}} = -m_{1}v_{1}} \atop {m_{3}v_{3_{\displaystyle y}} =- m_{2}v_{2}}} \right \bigg |:m_{3}$   $\displaystyle \left \{ { {v_{3_{\displaystyle x}} = -\dfrac{m_{1}v_{1}}{m_{3}} } \atop { {v_{3_{\displaystyle y}} = -\dfrac{m_{2}v_{2}}{m_{3}} }} \right.$

$v_{3} = \sqrt{v_{3_{\displaystyle x}}^{2} + v_{3_{\displaystyle y}}^{2} } = \sqrt{\left( -\dfrac{m_{1}v_{1}}{m_{3}}\right)^{2} + \left( -\dfrac{m_{2}v_{2}}{m_{3}} \right)^{2}} =\sqrt{\left( \dfrac{m_{1}v_{1}}{m_{3}}\right)^{2} + \left( \dfrac{m_{2}v_{2}}{m_{3}} \right)^{2}}$

${v_{3_{\displaystyle x}} = \dfrac{m_{1}v_{1}}{m_{3}} =$ (4 кг * 200 м/с) / 8 кг = 100 м/с

${v_{3_{\displaystyle y}} = \dfrac{m_{2}v_{2}}{m_{3}} =$ (9 кг * 50 м/с) / 8 кг = 56,25 м/с

$v_{3} =$ √(10 000 м²/с² + 3 164,0625 м²/с²) ≈ 115 м/c

Ответ: $v_{3} = 115$ м/c.