Предмет: Математика,
автор: chernorussia
показательные неравенства (срочно)
Приложения:
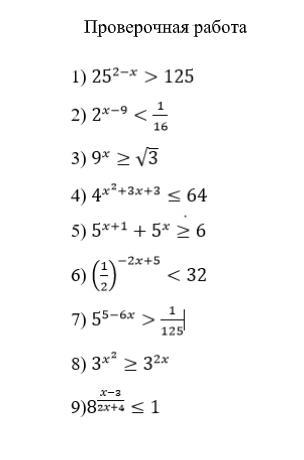
Ответы
Автор ответа:
1
!!!!!!!!!!!!!!!!!!!!!!!
Приложения:

Miroslava227:
В 4) посмотрите внимательнее, какую степень списали
там +3, а не +2
и у вас нет 8, 9
В 4) и решено правильно!!!!
8 и 9 не поместились, пишу с телефона и 2 фотки отсылать не получается...
А вообще-то мог и спасибо сказать!!!!
8 и 9 не поместились, пишу с телефона и 2 фотки отсылать не получается...
А вообще-то мог и спасибо сказать!!!!
А что так агрессивно?) (И это не мое задание, вас уже поблагодарил человек, который его добавил)
Я говорю, в 4) там 4 в степени x^2+3x+3, а не в x^2+3x+2
Посмотрите внимательнее
К тому же, я тоже с телефона все делаю, и можно добавлять 5 фотографий
Да, я была невнимательна, извини. Никакой агрессии не было, показалось....
Автор ответа:
1
Ответ:
х принадлежит [0;3].
х принадлежит (-беск;0]U[2;+беск).
х принадлежит (-2;3].
где дискриминант и решение его?
Думаю, решить квадратное уравнение не составит труда) здесь главное разобраться со показательными функциями
Похожие вопросы
Предмет: Алгебра,
автор: Anton982406
Предмет: Математика,
автор: jooo90
Предмет: Другие предметы,
автор: zhevelkov
Предмет: Математика,
автор: TitikØ
Предмет: Алгебра,
автор: mikyzz