Предмет: Алгебра,
автор: minalunnova
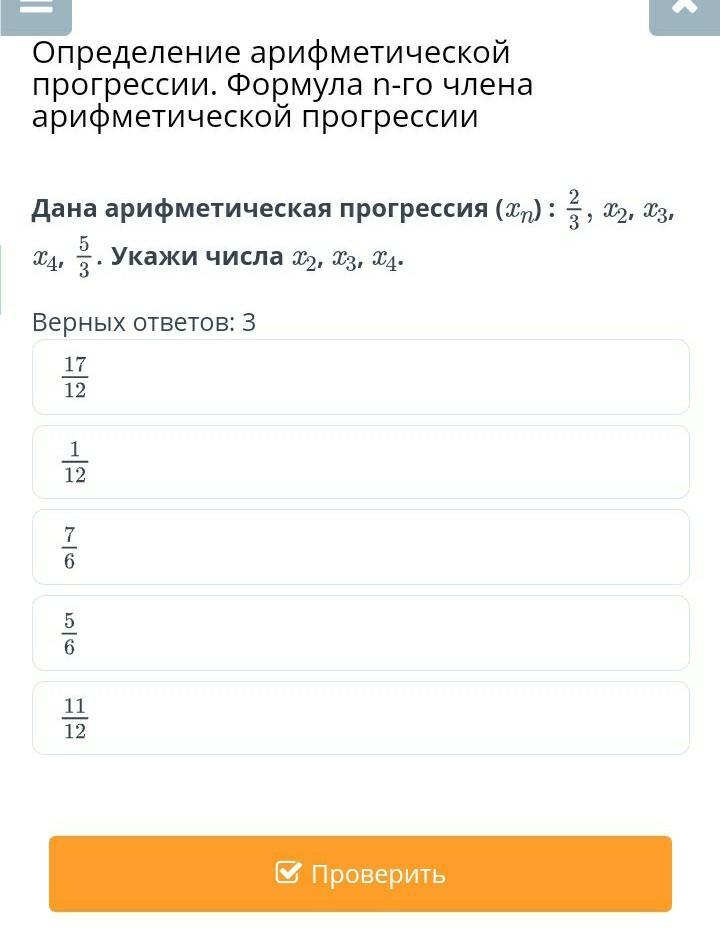
Дана арифметическая прогрессия (xn) : 2/3, x2, x3, x4, 5/3.
Укажи числа x2, x3, x4.
Верных ответов: 3
Приложения:
TiLox2020:
хочу решение
Ответы
Автор ответа:
3
Ответ и Объяснение:
По условию в арифметической прогрессии (): x₁ = 2/3 и x₅ = 5/3.
Общий член арифметической прогрессии определяется по формуле
где x₁ - первый член, а d - разность арифметической прогрессии.
По этой формуле
Подставим известные значения и находим разность d:
Теперь находим неизвестные члены арифметической прогрессии:
Похожие вопросы
Предмет: Химия,
автор: AGMLD
Предмет: Математика,
автор: lena0327
Предмет: Математика,
автор: Polinych
Предмет: Математика,
автор: AkulinaKonstantinova
Предмет: Математика,
автор: помогите1125