Предмет: Математика,
автор: prostotom
Дифференциальное исчисление функции нескольких переменных. Задание на скриншотах.
Приложения:

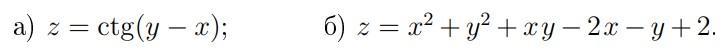
Ответы
Автор ответа:
1
Ответ:
1) :
а)
б)
2) :
а)
б)
Пошаговое объяснение:
Частная производная — это предел отношения приращения функции по выбранной переменной к приращению этой переменной, при стремлении этого приращения к нулю.
1) :
а)
б)
2) :
а)
б)
seihan:
пожалуйста ответь на мой вопрос
Похожие вопросы
Предмет: Русский язык,
автор: dasha898989
Предмет: Другие предметы,
автор: maksonчик
Предмет: Физика,
автор: AleksaZlo0901
Предмет: Алгебра,
автор: Мейти
Предмет: Математика,
автор: неумный21