Предмет: Геометрия,
автор: muxart0
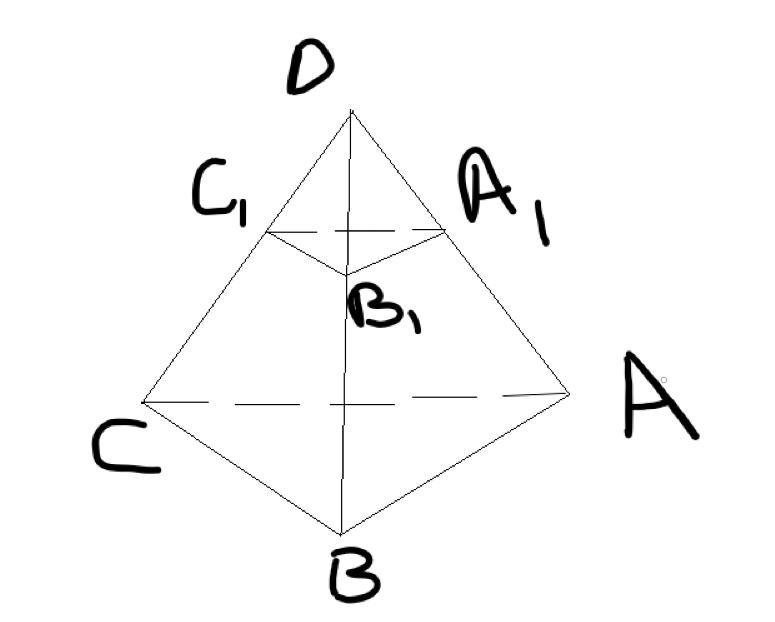
A1B1C1 || ABC, DA1 : AA1 = 3 : 4, S(A1B1C1)= 27
Найти S(ABC)
Приложения:
Ответы
Автор ответа:
2
A1B1C1 || ABC, DA1 : AA1 = 3 : 4, S(A1B1C1)= 27 . Найти S(ABC)
Объяснение:
1) Т.к. плоскости граней A1B1C1 и ABC параллельны , то А1С1║АС⇒ соответственные углы ∠DC1A1=∠DCA и ∠D-общий . Поэтому ΔDC1A1 ∼ DCA по 2 углам .В подобных треугольниках сходственные стороны пропорциональны : .
2) Т.к. A1B1C1 || ABC , то ΔA1B1C1 подобен ΔABC с коэффициентом
подобия , к=
. По т. об отношении площадей подобных треугольников
получаем или
, S(ABC)=12 ед².
muxart0:
а почему отношение DA1 и DA будет являться коэффициентом подобия?
я имею ввиду почему именно DA1 и DA, они ведь не являются частями треугольников
DA и DA1 это не части треугольников ABC и A1B1C1 как их отношение может быть К
Похожие вопросы
Предмет: Математика,
автор: низнайка2003
Предмет: Литература,
автор: миксерка
Предмет: Английский язык,
автор: pkochurowa
Предмет: Биология,
автор: Sinderella2006
Предмет: Химия,
автор: vadik33333333