Question

50 баллов
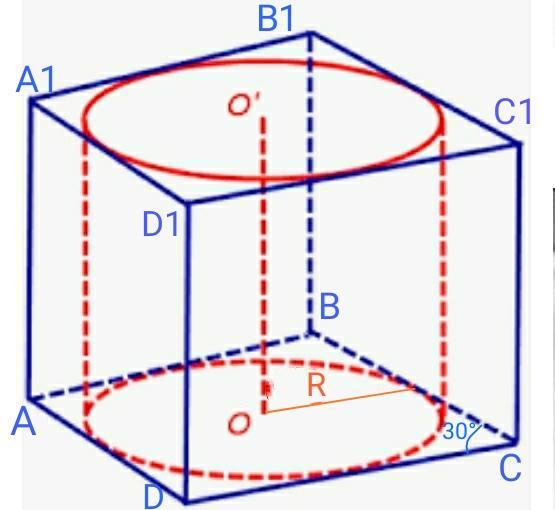
Основание прямой призмы — ромб с острым углом 30°, высота призмы равна 15 см.
Цилиндр с боковой поверхностью 135π см² вписан в призму.
Определи площадь боковой поверхности призмы.
Очень срочно!!!

Answer 1

Ответ:

1080см²

Объяснение:

Дано

Цилиндр

Sб.ц.=135π см² площадь боковой поверхности цилиндра.

ABCDA1B1C1D1- призма.

ABCD- ромб.

CC1=h=15см

<DCB=30°

Sб.пр.=?

Решение

Из формулы нахождения площади боковой поверхности цилиндра.

Sб.ц=2πRh, найдем радиус цилиндра.

R=Sб.ц./2πh

R=135π/2π15=135/30=4,5 см радиус цилиндра.

Из формулы

R=a*sin30°/2, где а- сторона ромба

а=ВС.

Найдем сторону ромба.

R=a/4

a=R*4=4*4,5=18 см сторона ромба

ВС=18 см

Р=4*ВС=4*18=72 см периметр ромба.

Sбок=Р*h=P*CC1=72*15=1080 см² площадь боковой поверхности призмы.