Предмет: Математика,
автор: Ireaperz
Решите уравнение с параметром (фотка)
Желательно, с подробным решением
Приложения:
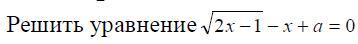
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: nemezida1
Предмет: Русский язык,
автор: anisinkova63
Предмет: Физика,
автор: Verge8
Предмет: Химия,
автор: Slavik1234Dom
Предмет: Химия,
автор: dizzix228dizzix