Question

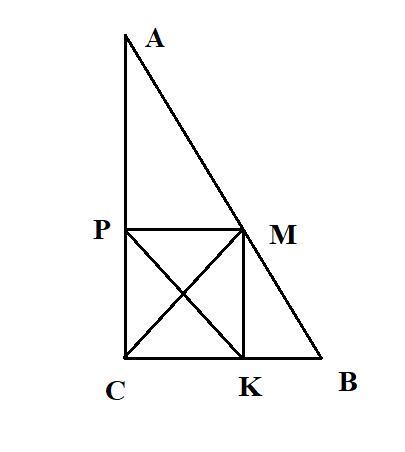
Среди всех точек гипотенузы AB прямоугольного треугольника ABC рассматривается такая точка M, что длина отрезка PK минимально возможна, где P и K – проекции точки M на катеты. Найдите |BC|², если AC=√10, PK=3.

Answer 1

Ответ:

|BC|² = 90

Объяснение:

PCKM - прямоугольник, поэтому PK = MC. Наименьшее расстояние CM (от точки C до прямой AB) - перпендикуляр из C на AB. По теореме Пифагора для ΔCAM, AM = √(10-9) = 1

ΔCAM подобен ΔBAC по 3 углам, поэтому AM/CM = AC/BC ⇒ 1/3 = √10/BC ⇒ BC = 3√10, |BC|² = 90