Question

Какую наибольшую целочисленную длину может иметь высота треугольника, если две другие высоты равны 10 и 15?

Answer 1

Ответ:

29 см

Объяснение:

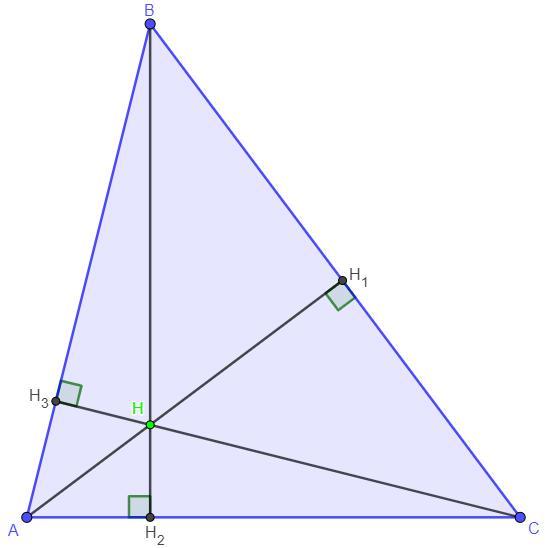
Дано: $BH_{2} = 15$ см, $CH_{3} = 10$ см, $AH_{1} \perp BC,$ $BH_{2} \perp AC$,$CH_{3} \perp AB$,$AH_{1} \in \mathbb N$

Найти: $max: AH_{1} -$ ?

Решение: Площадь треугольника равняется половине произведения высоты на сторону к которой она проведена. Составим системе уравнений, где выразим площадь треугольника через соответствующие стороны и высоты.

$\left \{\begin{array}{l} S_{\bigtriangleup ABC} = \dfrac{AH_{1} * BC}{2} \\ S_{\bigtriangleup ABC} = \dfrac{BH_{2} * AC}{2} \\ S_{\bigtriangleup ABC} = \dfrac{CH_{3} * AB}{2}\end{array} \right.$

Выразим из системы стороны треугольника через высоты и площадь.

$\left \{\begin{array}{l} S_{\bigtriangleup ABC} = \dfrac{AH_{1} * BC}{2} \\ S_{\bigtriangleup ABC} = \dfrac{BH_{2} * AC}{2} \\ S_{\bigtriangleup ABC} = \dfrac{CH_{3} * AB}{2}\end{array} \right. \bigg| * 2$  $\left \{\begin{array}{l} 2S_{\bigtriangleup ABC} = AH_{1} * BC} |:AH_{1} \\ 2S_{\bigtriangleup ABC} = BH_{2} * AC|:BH_{2} \\ 2S_{\bigtriangleup ABC} = CH_{3} * AB|:CH_{3}\end{array} \right.$

$\left \{\begin{array}{l} BC = \dfrac{2S_{\bigtriangleup ABC}}{AH_{1}} \\ AC = \dfrac{2S_{\bigtriangleup ABC}}{BH_{2}} \\ AB = \dfrac{2S_{\bigtriangleup ABC}}{CH_{3}}\end{array} \right.$

Так как $AH_{1}$ - высота треугольника, то $AH_{1} > 0$.

Если треугольник существует, то выполняется неравенство треугольника и каждый треугольник имеет площадь.  

Неравенство треугольника для треугольника ΔABC:

$\left \{\begin{array}{l} AB < AC + CB \\ AC < AB + BC \\ BC < BA + AC\end{array} \right$ $\left \{\begin{array}{l} \dfrac{2S_{\bigtriangleup ABC}}{CH_{3}} < \dfrac{2S_{\bigtriangleup ABC}}{BH_{2}} +\dfrac{2S_{\bigtriangleup ABC}}{AH_{1}} \\ \dfrac{2S_{\bigtriangleup ABC}}{BH_{2}} < \dfrac{2S_{\bigtriangleup ABC}}{CH_{3}} +\dfrac{2S_{\bigtriangleup ABC}}{AH_{1}} \\ \dfrac{2S_{\bigtriangleup ABC}}{AH_{1}} < \dfrac{2S_{\bigtriangleup ABC}}{CH_{3}} + \dfrac{2S_{\bigtriangleup ABC}}{BH_{2}}\end{array} \right \bigg| : 2S_{\bigtriangleup ABC}$

$\left \{\begin{array}{l} \dfrac{1}{CH_{3}} < \dfrac{1}{BH_{2}} +\dfrac{1}{AH_{1}} \\ \dfrac{1}{BH_{2}} < \dfrac{1}{CH_{3}} +\dfrac{1}{AH_{1}} \\ \dfrac{1}{AH_{1}} < \dfrac{1}{CH_{3}} + \dfrac{1}{BH_{2}}\end{array} \right$  $\left \{\begin{array}{l} \dfrac{1}{10} < \dfrac{1}{15} +\dfrac{1}{AH_{1}} \\ \dfrac{1}{15} < \dfrac{1}{10} +\dfrac{1}{AH_{1}} \\ \dfrac{1}{AH_{1}} < \dfrac{1}{10} + \dfrac{1}{15}\end{array} \right$  $\left \{\begin{array}{l} \dfrac{1}{10} - \dfrac{1}{15} < \dfrac{1}{AH_{1}} \\ \dfrac{1}{15}-\dfrac{1}{10} < \dfrac{1}{AH_{1}} \\ \dfrac{1}{AH_{1}} < \dfrac{1}{10} + \dfrac{1}{15}\end{array} \right$

$\left \{\begin{array}{l} \dfrac{3 - 2}{30} < \dfrac{1}{AH_{1}} \\ \dfrac{2 - 3}{30} < \dfrac{1}{AH_{1}} \\ \dfrac{1}{AH_{1}} <\dfrac{3 + 2}{30}\end{array} \right$  $\left \{\begin{array}{l} \dfrac{1}{30} < \dfrac{1}{AH_{1}} \\ -\dfrac{1}{30} < \dfrac{1}{AH_{1}} \\ \dfrac{1}{AH_{1}} <\dfrac{5}{30}\end{array} \right$ $\left \{\begin{array}{l} \dfrac{1}{30} < \dfrac{1}{AH_{1}} \\ -\dfrac{1}{30} < \dfrac{1}{AH_{1}} \\ \dfrac{1}{AH_{1}} <\dfrac{1}{6}\end{array} \right \bigg| * AH_{1}$ $\left \{\begin{array}{l} \dfrac{AH_{1}}{30} < 1|*30\\ -\dfrac{AH_{1}}{30} < 1|*30\\ 1<\dfrac{AH_{1}}{6}|*6\end{array} \right$

$\left \{\begin{array}{l} AH_{1} < 30\\ -AH_{1} < 30|*(-1)\\ 6<AH_{1}\end{array} \right$$\left \{\begin{array}{l} AH_{1} < 30\\ AH_{1} > -30\\ 6<AH_{1} \\ AH_{1} > 0 \end{array} \right \Longrightarrow AH_{1} \in (6;30)$

Так как  $\left \{\begin{array}{l} AH_{1} \in \mathbb N \\ AH_{1} \in (6;30)\end{array} \right. \Longrightarrow max:AH_{1} = 29$ см.