Предмет: Геометрия,
автор: nakularb
Диагонали параллелограмма равны 10 и 26, а угол между
ними равен 30. Найдите площадь этого параллелограмма.
Ответы
Автор ответа:
5
Ответ:
Объяснение:
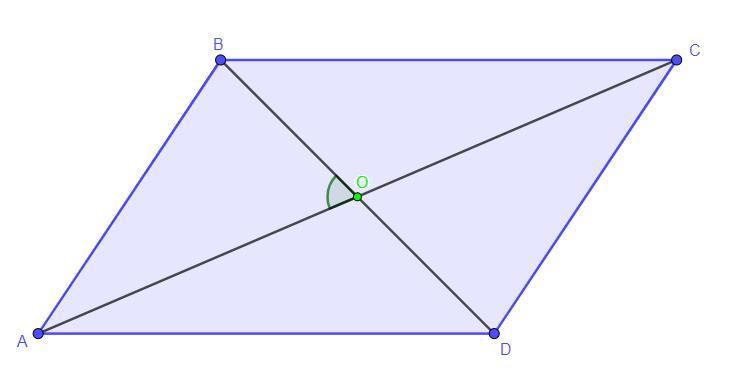
Дано: ABCD - параллелограмм, BD = 10, AC = 26, ∠AOB = 30°
Найти: ?
Решение: Так как ABCD - параллелограмм по условию, то ABCD - выпуклый четырехугольник. По формуле площади выпуклого четырехугольника: квадратных единиц.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: gjhjhgjhjh
Предмет: Математика,
автор: Sexi902
Предмет: Английский язык,
автор: 71727
Предмет: Математика,
автор: ekaterinaleskina
Предмет: Химия,
автор: Глупая78