Предмет: Математика,
автор: declunya
Разложить многочлен на линейные множители. ( 10 номер)
Приложения:
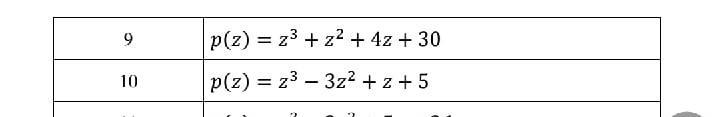
Ответы
Автор ответа:
0
Ответ:
p(z)=(z+1)(z-2-i)(z-2+i)
Пошаговое объяснение:
p(z)=z³-3z²+z+5;
z³-3z²+z+5=0;
Все делители свободного члена: ±1;±5.
z=1; 1³-3*1²+1+5≠0;
z=-1; -1-3-1+5=0; один из корней многочлена -1. Следовательно один из множителей выглядит так (z+1).
Разделим p(z) на множитель (z+1):
z³-3z+z+5 l z+1
z³+z² l z²-4z+5
z³+z²
-4z²+z
-4z²-4z
5z+5
5z+5
0
p(z)=(z+1)(z²-4z+5);
z²-4z+5=0; D=16-20=-4; z₂₃=0.5(4±√(-4)); z₂=2+i; z₃=2-i;
p(z)=(z+1)(z-2-i)(z-2+i)
Похожие вопросы
Предмет: Химия,
автор: nagornaya1801
Предмет: Английский язык,
автор: rasyanova79
Предмет: Алгебра,
автор: Myxa123123
Предмет: Литература,
автор: Cealdre
Предмет: Биология,
автор: JAM0709