Предмет: Алгебра,
автор: vtf17
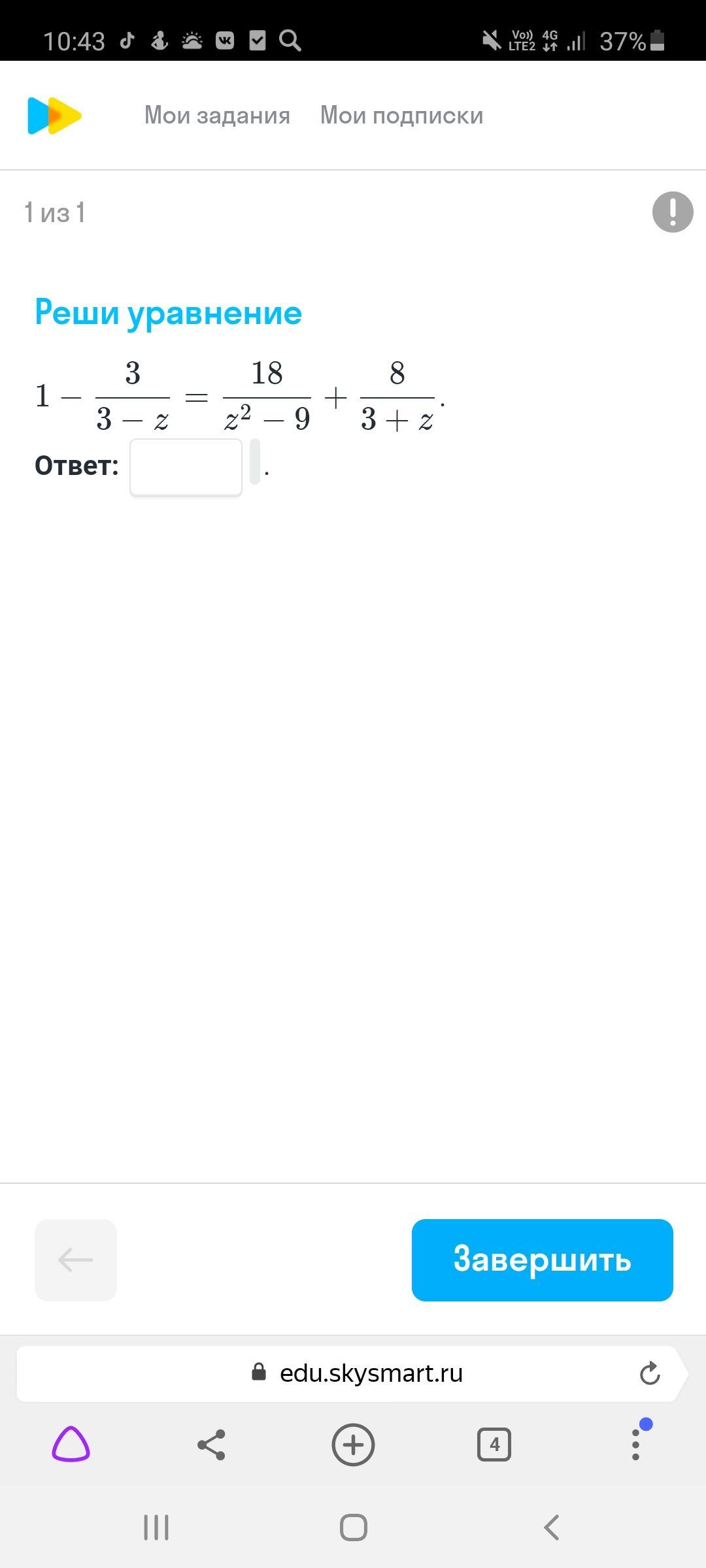
Помогите решить пожалуйста, у меня получается два, но не правильно пишет
Приложения:
Ответы
Автор ответа:
1
Проверка :
Автор ответа:
1
Ответ:
Объяснение:
ОДЗ:
Решение:
Корень z₂ не удовлетворяет ОДЗ.
Похожие вопросы
Предмет: Алгебра,
автор: svi98
Предмет: Математика,
автор: dfrtyujn
Предмет: Английский язык,
автор: geseinovat
Предмет: Математика,
автор: topo121
Предмет: Обществознание,
автор: lvardanyan1