Срочно!! Даю 15 баллов!
З вершини тупого кута ромба ABCD проведено висоти BM і BN , причому відрізок MN вдвічі менший за діагональ BD. Знайдіть кути ромба.
Ответы
Ответ:
2 по 30°, и 2 по 150°
если нужно объяснение почему так обязательно напишу
объяснение:
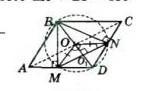
что бы было понятней прикрепила рисунок по которому будем делать
Для розв'язання задачі проводимо коло з центром в т. О. BNDM — вписаний чотирикутник,
< BND= <BMD=90°, тобто <М+<N=180°.
Маємо <В + <D=180° (<M+<B+<N+<D=360°, то <B≠<D=180°)
Розглянемо <BND=90° і <BMD =90°— вписані кути, які спираються на діаметр. Тобто ОВ=ON=OD=OM=BD/2
Розглянемо ∆МON — рівнобедрений за означенням, OM=ON, то OO1— медіана, бісектриса, висота, МО1=О1N=1/4 всієї BD.
Тобто із ∆ ВО1N прямокутного маємо: ON=OF=BD/2, O1N=BD/4.
Тобто гіпотенуза в два рази більша за катетом.
Маємо <NOO1 =30°, тобто <MON=60°, <MDN— вписаний кут, який спирається на дугу МВN=360°-60°=300°, тобто <D=300°÷2=150°, <D=<В=150°. маємо<А=<С=180°-150°=30°(за властивістю ромба про рівні паралельні кути)
ну и ответ есть сверху