Предмет: Алгебра,
автор: gorodilka06
Помогите решить!!!! Даю 100 баллов! (по действиям с пояснением)
1) =
=
2)
Ответы
Автор ответа:
1
Ответ:
решение на фото в приложении
Приложения:
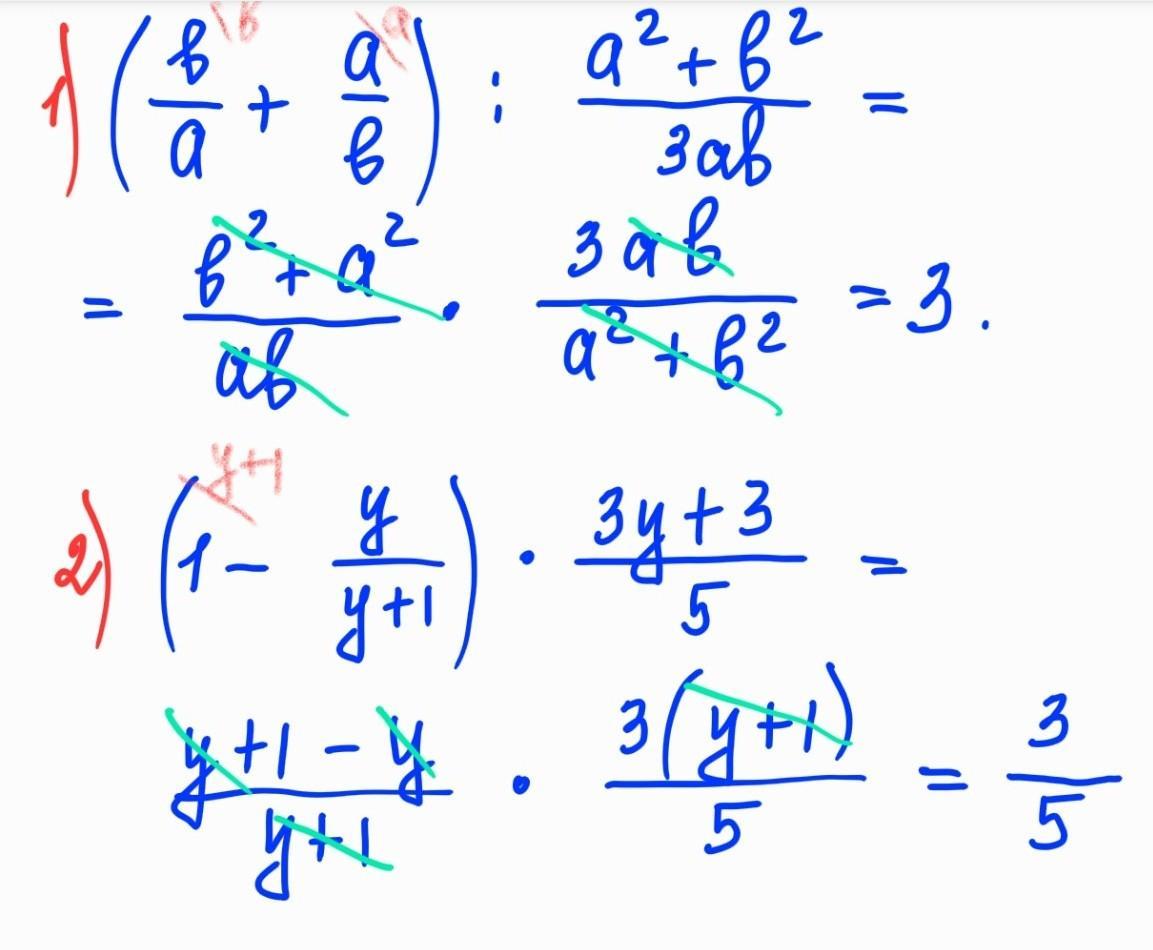
gorodilka06:
было указано по действиям
Автор ответа:
1
Ответ:
Объяснение:
1. Сначала выполним сложение в скобках. Общий знаменатель двух дробей:
Дополнительный множитель для первой дроби:
Дополнительный множитель для второй дроби:
2. Деление на дробь равносильно умножению на обратную дробь:
Ответ: 3.
1. Сначала выполним вычитание в скобках. Единицу представим как дробь со знаменателем 1:
Общий знаменатель двух дробей:
Дополнительный множитель для первой дроби:
Дополнительный множитель для второй дроби:
2. Вынесем тройку за скобки в числителе второй дроби:
Ответ: 0,6.
Похожие вопросы
Предмет: Математика,
автор: perevertovalen
Предмет: Математика,
автор: Tekirikanok
Предмет: Алгебра,
автор: eelez
Предмет: География,
автор: АлисаТян2006
Предмет: Литература,
автор: sanekzv12