Предмет: Алгебра,
автор: matveishogolev
Известно,что f(x) = 3x^2+2x-3
Докажите, что f(cosx)=2cosx-3sinx^2
И, если не трудно, объясните, как это работает)
Ответы
Автор ответа:
1
Ответ:
Объяснение:
В формулу 3x²+2x-3 подставляем cosx вместо x.
f(cosx) = 3cosx^2 + 2cosx - 3. Нужно доказать, что:
3cosx^2 + 2cosx - 3 = 2cosx-3sinx^2
3cosx^2-3 = -3sinx^2 (вычли 2cosx)
cosx^2-1 = -sinx^2 (сократили на 3)
cosx^2 + sinx^2 = 1
Получили основное тригонометрическое тождество. Оно верно, значит и то, что нужно было доказать, верно.
Автор ответа:
1
Ответ:
доказательство показано на фото в приложении
Приложения:
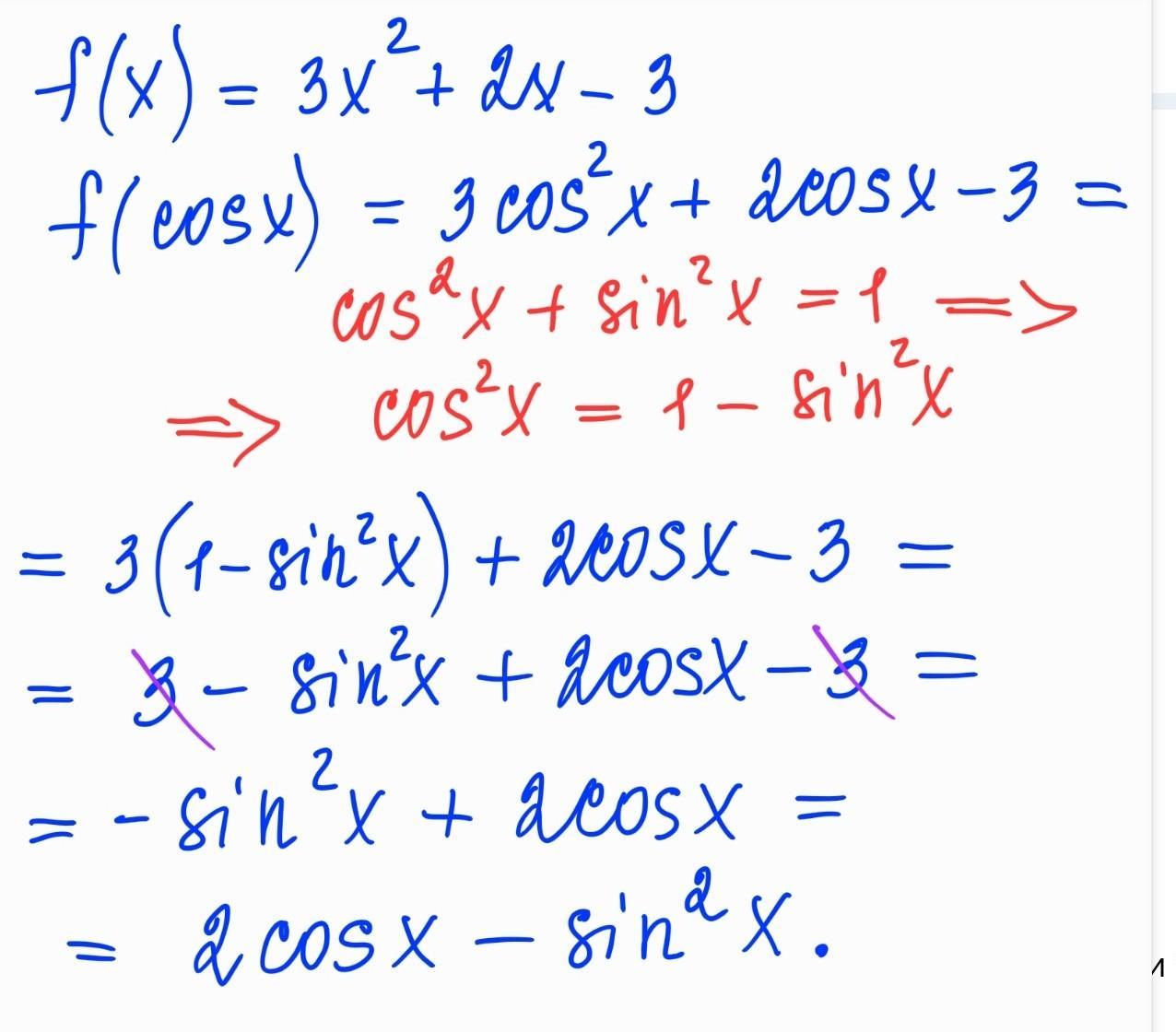
Похожие вопросы
Предмет: Математика,
автор: titovalelye
Предмет: Математика,
автор: оленька0303
Предмет: Геометрия,
автор: sysuevanastya
Предмет: Математика,
автор: Raf234
Предмет: Математика,
автор: llllll13