Question

знайти площу квадрата, вписаного в коло, якщо площа правильного шестикутника, вписаного в це коло, дорівнює 6 корінь 3

Answer 1

Ответ:

Площадь квадрата равна 8 ед²

Объяснение:

Дано

Окружность

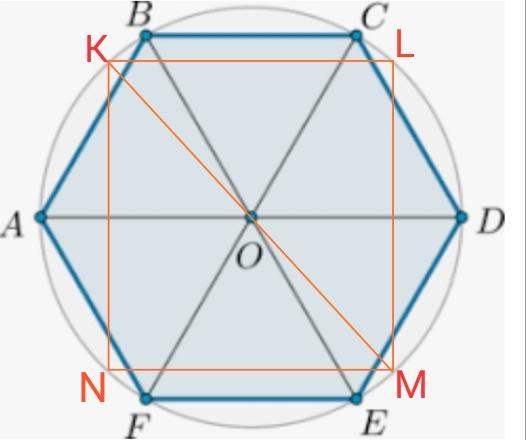
АBCDEF- шестиугольник вписанный

KLMN- квадрат вписанный.

SABCDEF=6√3 ед²

SKLMN=?

Решение

Шестиугольник состоит из 6 равносторонних треугольников.

Найдем площадь одного треугольника.

S∆ABO=SABCDEF/6=6√3/6=√3 eд² площадь одного треугольника.

Из формулы равностороннего треугольника

S=a²√3/4, где а -сторона треугольника.

Найдем сторону треугольника.

а=√(4S/√3)=√(4√3/√3)=2 ед сторона треугольника

а=АО=R=2ед.

КМ диагональ квадрата равна диаметру окружности.

КМ=2*АО=2*2=4 ед. диагональ квадрата.

Из формулы нахождения диагонали квадрата

КМ=КN*√2.

Найдем сторону квадрата.

КN=KM/√2=4/√2=2√2 сторона квадрата.

SKLMN=KN²=(2√2)²=4*2=8 ед² площадь квадрата