Question

Решите систему неравенств:
cos t>0
sin t<-1/2​

Answer 1

Ответ:

Объяснение:

Ответ:

Объяснение:

cos t>0                             -п/2  <  t   < п/2

Косинус положителен в первой и четвертой четвертях

Синус отрицателен в третьей и четвертой четвертях.

sin t < -1/2   

   ( sin(-π/6)  =sin (-5π/6)=-1/2 )  

            -5п/6  <  t   < -п/6

Решая систему ,сводим оба ответа вместе на числовой оси

      и получаем    -п/2  <  t   <  -п/6                             

    -5п/6  <    -п/2  <  t   <  -п/6    < п/2

_____₀_______₀<<<<<<<<<<₀______₀______

Добавим к обеим частям по полному периоду 2п

  -п/2+2п  <  t   <  -п/6   +2п  

3п/2    <  t   <  11п/6    ,(вместо 1 5/6 я написал 11/6 ,чтобы не спутали запись с целой частью и дробью)

Добавив к обеим частям 2пк получим полное решение в общем виде.

3п/2 +2пк   <  t   <  11п/6 +2пк

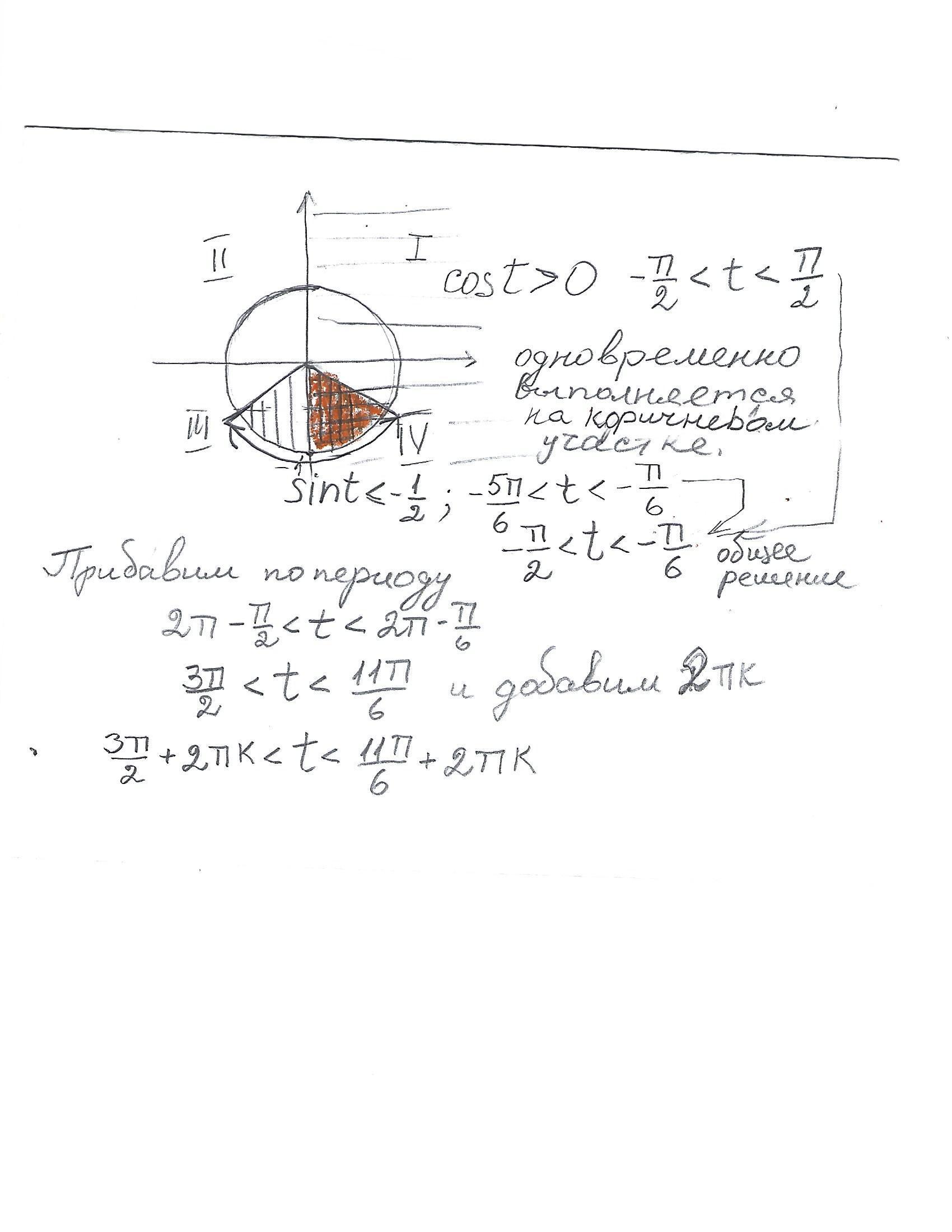
 В приложении есть пояснение с помощью единичного круга .

Горозонтально заштрихована первая и четвертая четверти в которых cos t>0  

Вертикально заштрихована та область в которой sin t < -1/2  

половина этой области попадает в область заштрихованную коричневым ,то есть в ней и синус меньше -0,5 и косинус больше 0.

Это и есть наше искомое решение.

 3п/2 +2пк   <  t   <  11п/6 +2пк