Предмет: Алгебра,
автор: radivan778
Срочно,10 минут до конца
Приложения:
Ответы
Автор ответа:
1
Ответ:
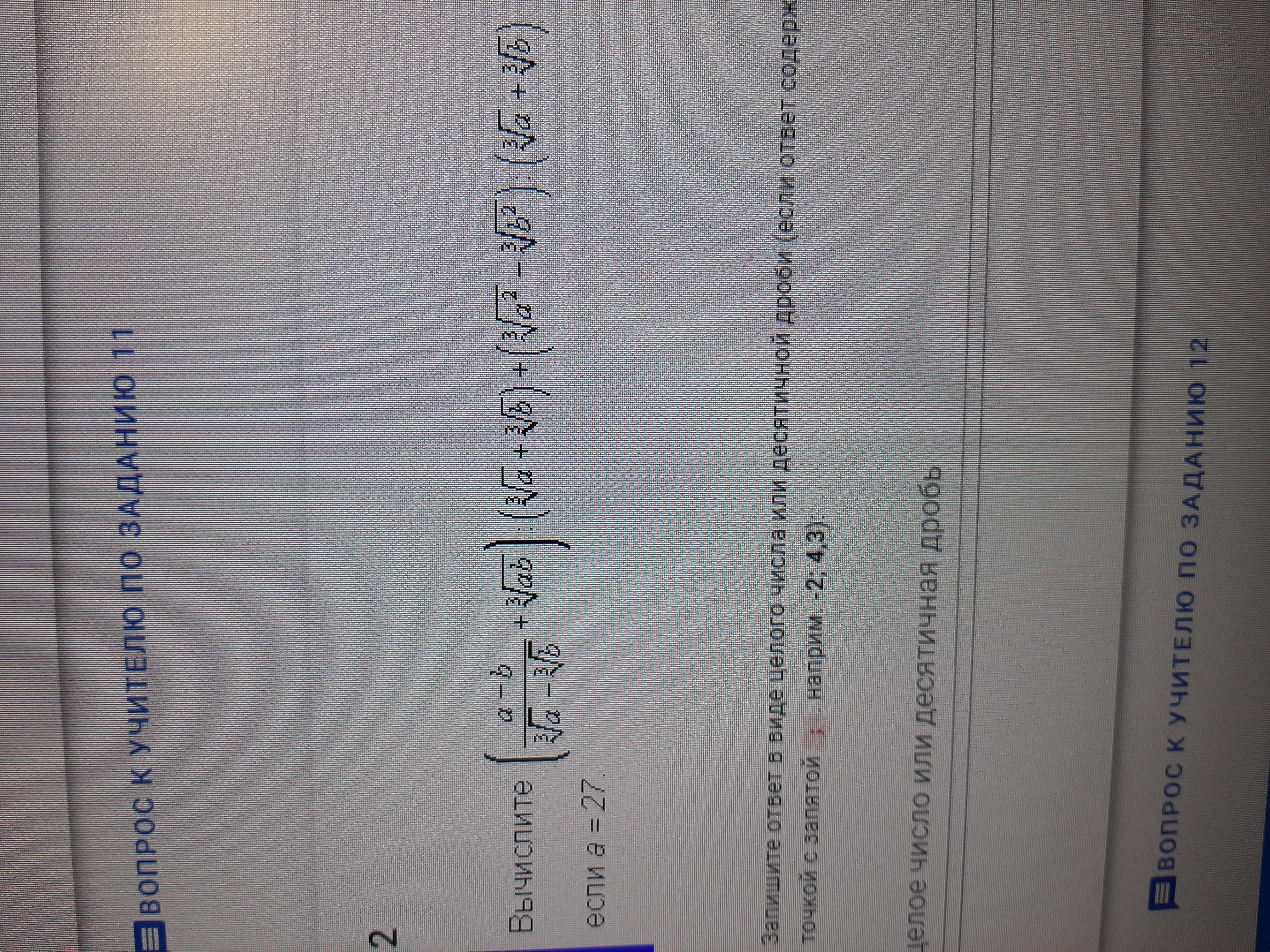
2) С начала надо упростить выражение:
Теперь подставим значение под упрощённое выражение:
Похожие вопросы
Предмет: Математика,
автор: Мелина24
Предмет: Русский язык,
автор: albiertgalimov
Предмет: Математика,
автор: ZeniMax155
Предмет: Алгебра,
автор: aryyyyyyn
Предмет: Математика,
автор: Серюля