Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста!!!
Приложения:
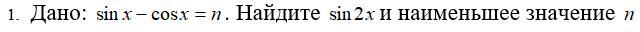
Ответы
Автор ответа:
0
Ответ:
sin(2x) = 1 - n², минимальное n = -√2
Объяснение:
sin(2x) = 2*sin(x)*cos(x)
Заметим, что n² = sin^2(x) + cos^2(x) - 2sin(x)cos(x) = 1 - 2sin(x)cos(x) (осн. тригоном. тожд.). Значит, 2sin(x)cos(x) = 1 - n². sin(2x) = 1 - n².
1 - n² ≤ 1 ⇒ n² ≥ 0 ⇒ n - любое число
1 - n² ≥ -1 ⇒ n² ≤ 2 ⇒ n ∈ [-√2;√2]
Значит, минимальное значение n = -√2
Похожие вопросы
Предмет: Литература,
автор: Eva250001
Предмет: Русский язык,
автор: shekhtovaaaaaaa
Предмет: Русский язык,
автор: Milena25023
Предмет: Математика,
автор: melkii80
Предмет: Химия,
автор: sam128