Предмет: Математика,
автор: mettatonneoo
Сложение смешанных чисел. Вычитание смешанных чисел. Урок 2
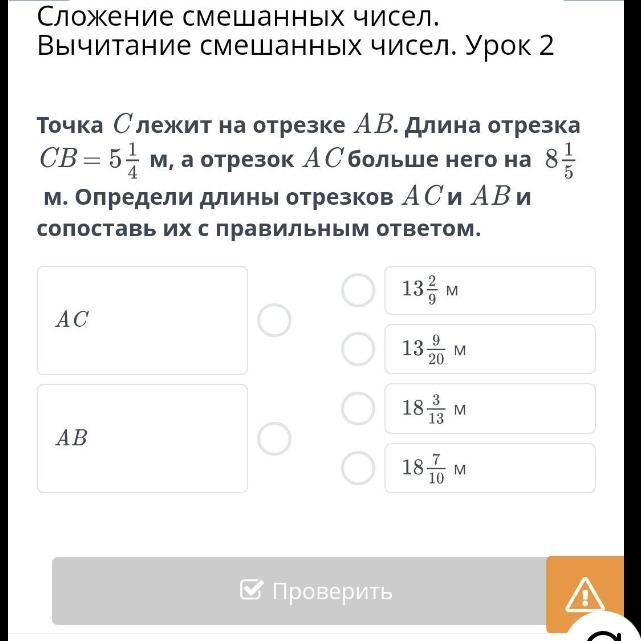
Точка C лежит на отрезке AB. Длина отрезка CB =
м, а отрезок AC больше него на
м. Определи длины отрезков AC и AB и сопоставь их с правильным ответом.
Те кто уже прошли этот тест, помогите если есть возможность
Приложения:
спс
чел в коментариях спс за ответ лучший!
Ответы
Автор ответа:
1
Ответ:
м,
м.
Пошаговое объяснение:
По условию
м, а отрезок АС на
м больше.
Найдем длину отрезка АС
м.
Так как точка С лежит на отрезке АВ, то длина отрезка АВ равна сумме длин отрезков АС и CB.
м.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: gusarovaoksana77
Предмет: Обществознание,
автор: Vadik51
Предмет: Русский язык,
автор: kisa15235
Предмет: Математика,
автор: Layka2005
Предмет: Алгебра,
автор: amN10
AB 18 7/10