Предмет: Алгебра,
автор: nneeeett
∫![\frac{dx}{\sqrt[3]{8x} } \frac{dx}{\sqrt[3]{8x} }](https://tex.z-dn.net/?f=%5Cfrac%7Bdx%7D%7B%5Csqrt%5B3%5D%7B8x%7D+%7D)
Помогите решить пожалуйста.
Прошу максимально подробно потому,что хочу понять как решать.
30 баллов
Заранее благодарю!
Приложения:
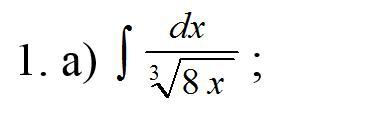
nneeeett:
Ну помогите пожалуйста хоть кто-нибудь :,(
аууу
:(
Ответы
Автор ответа:
0
Интеграл табличный..
Автор ответа:
0
Ответ:
Объяснение:
Похожие вопросы
Предмет: Физика,
автор: Nika19715
Предмет: Биология,
автор: Машуля011
Предмет: Литература,
автор: anastasiyaplot1
Предмет: Химия,
автор: malckob90oyp5bs