Предмет: Геометрия,
автор: ucheba7503
Основание прямой призмы - прямоугольный треугольник с гипотенузой 12см и катетом 5см. Найдите площадь боковой поверхности, если грань содержащая больший катет - квадрат.
Ответы
Автор ответа:
4
Ответ:
119+17√119 см²
Объяснение:
Дано:
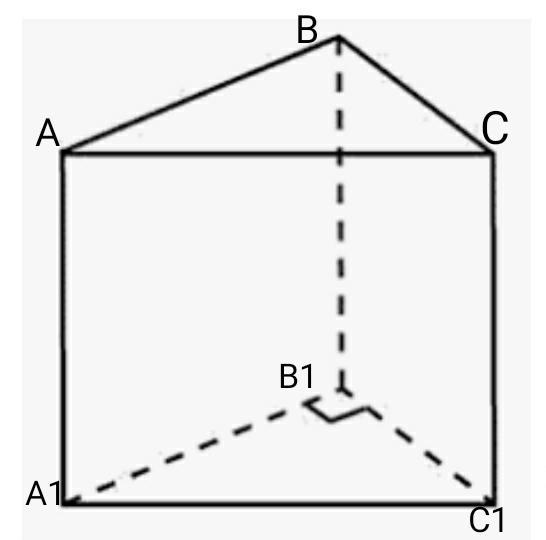
ABCA1B1C1- прямая призма.
∆А1В1С1- прямоугольный.
А1В1=5см
А1С1=12см.
Sбок=?
Решение.
По теореме Пифагора найдем второй катет ∆А1В1С1
С1В1²=А1С1²-А1В1²=12²-5²=144-25=119 см
С1В1=√119 см
√25<√119
5<√119 значит
ВВ1С1С является квадрат.
ВВ1=В1С1=С1С=ВС
ВВ1=√119см высота призмы.
Формула нахождения площади боковой поверхности призмы.
Sбок=Росн*h, где Росн- периметр основания, h=BB1 - высота.
Росн=А1В1+В1С1+А1С1=12+5+√119=
=17+√119 см периметр треугольника.
Sбок=(17+√119)*√119=17√119+119 см² площадь боковой поверхности призмы.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Herobrineeeeeee
Предмет: Математика,
автор: karina290909
Предмет: Химия,
автор: hana20011374
Предмет: Математика,
автор: олегзакон
Предмет: Математика,
автор: yulyagaevskayaoz1uaa