Предмет: Геометрия,
автор: muhammadsodikkahhoro
Найдите боковую сторону равнобедренной трапеции, изображённой на рисунке, в которой длина диагонали равна длине большего основания
Приложения:
Ответы
Автор ответа:
2
Ответ:
8см
Объяснение:
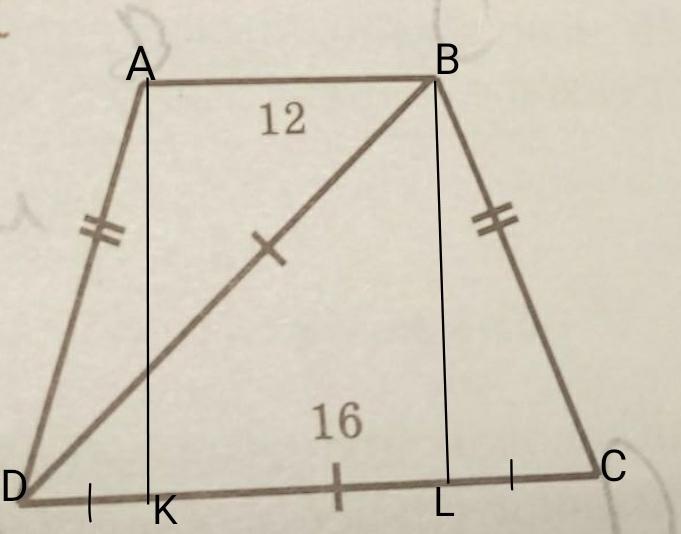
Дано:
ABCD- трапеция
AD=BC
DB=DC=16см
AB=12см
AD=?
Решение:
Проведём две высоты АК и ВL
AB=KL=12см (АВКL- прямоугольник; противоположные стороны равны)
DK=LC; (трапеция равнобедренная; проекции боковой стороны на нижнее основание равны, также как и боковые стороны трапеции)
LC=(DC-KL)/2=(16-12)/2=4/2=2см
DL=DC-LC=16-2=14см
Рассмотрим треугольник ∆DBL- прямоугольный.
DB- гипотенуза
DL и ВL - катеты.
По теореме Пифагора найдем ВL
ВL²=DB²-DL²=16²-14²=256-196=60
BL=√60 см
Рассмотрим треугольник ∆BLC- прямоугольный.
ВС- гипотенуза
ВL и LC - катеты.
По теореме Пифагора найдем ВС.
ВС²=BL²+LC²=(√60)²+2²=60+4=64см
BC=√64=8см
ВС=AD, по условию.
AD=8см
ВС=8см
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: annaalekseeva18
Предмет: Математика,
автор: kolosovaludmil
Предмет: История,
автор: екатерина47
Предмет: Алгебра,
автор: sasharbrb
Предмет: Математика,
автор: 4класс53