Предмет: Алгебра,
автор: dumpmac
Решите пожалуйста хоть ,что нибудь.
Приложения:

Ответы
Автор ответа:
0
№ 4.
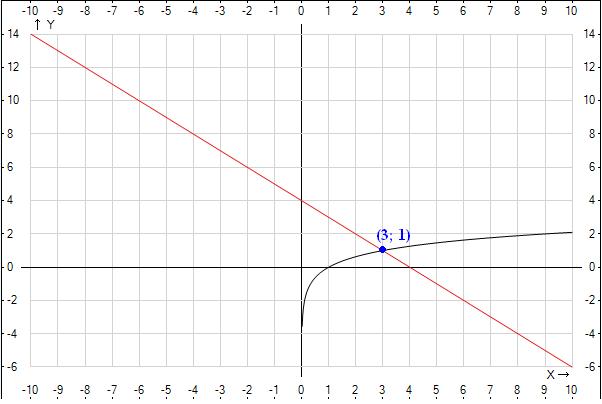
log3(x) = 4 - x
слева - логарифмическая функция
справа - линейная
решение - точка пересечения этих графиков.
По графикам видно (см. рисунок), что решением является точка: x = 3, y = 1
№ 5.
(1 - cosa + cos(2a)) / (sin(2a) - sina) = (1 - cosa + 2cos^2(a) - 1) / (2sina*cosa - sina) = cosa*(2cosa - 1) / (sina*(2cosa - 1)) = cosa / sina = ctga
№ 6.
(4 - x^2) / (2x - 3) > 0
1) Система: 4 - x^2 > 0 и 2x - 3 > 0
-2 < x < 2 и x > 1.5
Общее решение: 1.5 < x < 2
2) Система: 4 - x^2 < 0 и 2x - 3 < 0
x < -2, x > 2 и x < 1.5
Общее решение: x < -2
Ответ: x = (-бесконечность; -2) U (1.5; 2)
№ 7.
2cos(x/3 + pi/5) = sqrt2
cos(x/3 + pi/5) = sqrt2/2
x/3 + pi/5 = pi/4 + 2pi*k, x/3 = pi/20 + 2pi*k, x = 3pi/20 + 6pi*k
x/3 + pi/5 = - pi/4 + 2pi*k, x/3 = -9pi/20 + 2pi*k, x = -27pi/20 + 6pi*k
№ 8.
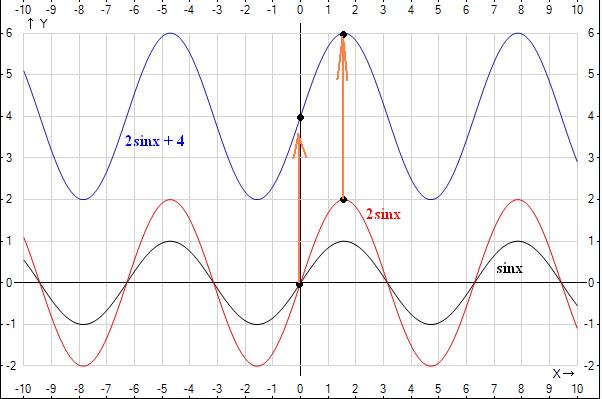
y = 2sinx + 4
Преобразования: sinx -> 2sinx (график сжали в два раза) -> 2sinx + 4 (график подняли на 4 единицы вверх) (см. рисунок)
log3(x) = 4 - x
слева - логарифмическая функция
справа - линейная
решение - точка пересечения этих графиков.
По графикам видно (см. рисунок), что решением является точка: x = 3, y = 1
№ 5.
(1 - cosa + cos(2a)) / (sin(2a) - sina) = (1 - cosa + 2cos^2(a) - 1) / (2sina*cosa - sina) = cosa*(2cosa - 1) / (sina*(2cosa - 1)) = cosa / sina = ctga
№ 6.
(4 - x^2) / (2x - 3) > 0
1) Система: 4 - x^2 > 0 и 2x - 3 > 0
-2 < x < 2 и x > 1.5
Общее решение: 1.5 < x < 2
2) Система: 4 - x^2 < 0 и 2x - 3 < 0
x < -2, x > 2 и x < 1.5
Общее решение: x < -2
Ответ: x = (-бесконечность; -2) U (1.5; 2)
№ 7.
2cos(x/3 + pi/5) = sqrt2
cos(x/3 + pi/5) = sqrt2/2
x/3 + pi/5 = pi/4 + 2pi*k, x/3 = pi/20 + 2pi*k, x = 3pi/20 + 6pi*k
x/3 + pi/5 = - pi/4 + 2pi*k, x/3 = -9pi/20 + 2pi*k, x = -27pi/20 + 6pi*k
№ 8.
y = 2sinx + 4
Преобразования: sinx -> 2sinx (график сжали в два раза) -> 2sinx + 4 (график подняли на 4 единицы вверх) (см. рисунок)
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Egorova2374
Предмет: Музыка,
автор: starling2911
Предмет: Русский язык,
автор: bolsaevairina
Предмет: Химия,
автор: маша443322
Предмет: Математика,
автор: Аноним