Предмет: Геометрия,
автор: ПопрошакинО
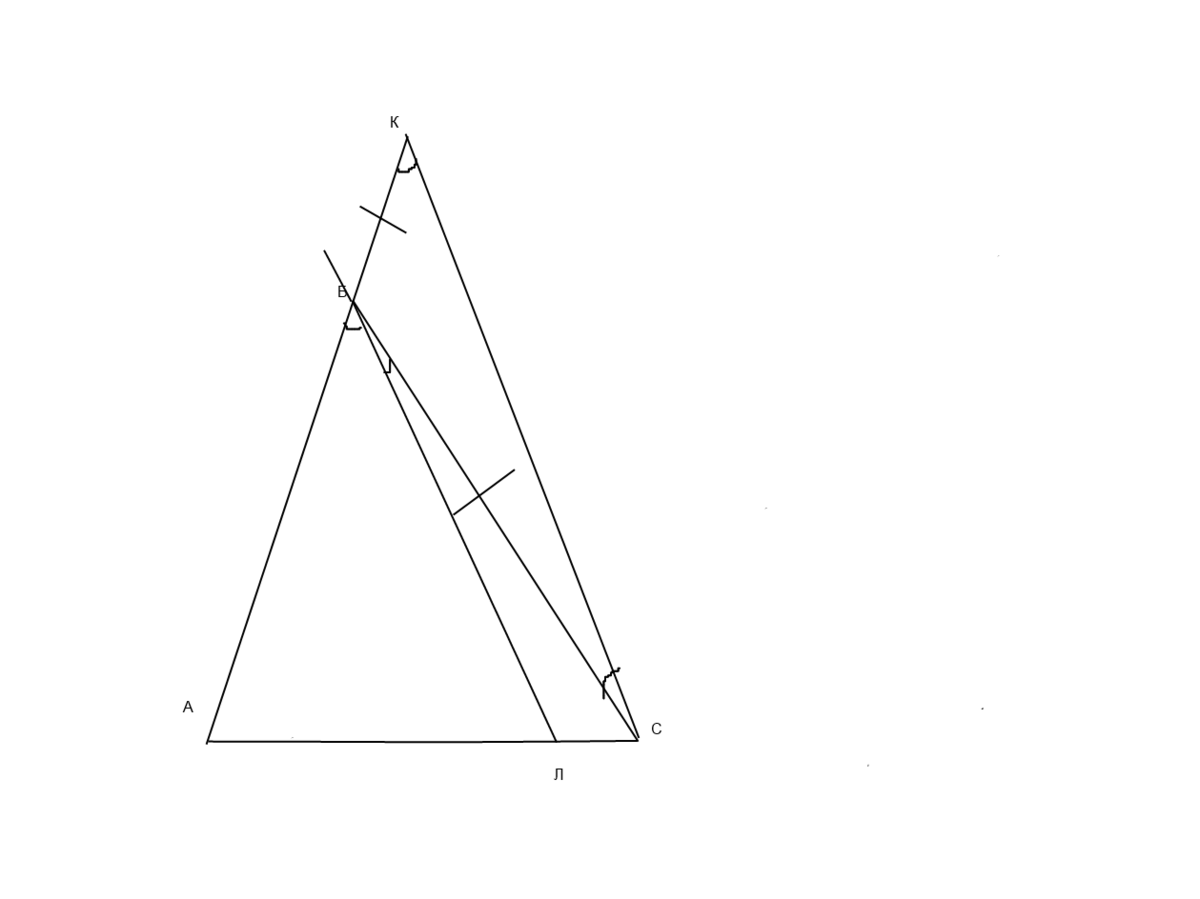
На продолжении стороны АВ треугольника АВС отложен отрезок ВК, равный ВС. На стороне АС выбрана точка L, так что отрезок BL параллелен CK. Докажите, что BL - биссектриса треугольника АВС.
Ответы
Автор ответа:
0
Треугольник СКБ-равнобедренный значит угол КСБ= углу СКБ
БЛ парралельна КС значит накрест лежащие углы равны и значит угол ЛБС= углу КСБ при секущей БС.
Угол АБЛ= углу СКБ пи секущей АК.
Исходя из всего угол АБЛ= углу ЛБС
БЛ парралельна КС значит накрест лежащие углы равны и значит угол ЛБС= углу КСБ при секущей БС.
Угол АБЛ= углу СКБ пи секущей АК.
Исходя из всего угол АБЛ= углу ЛБС
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: playgamesansar
Предмет: Обществознание,
автор: ulyamoresleep
Предмет: Химия,
автор: aizoka123